scipy.special.it2struve0#
- scipy.special.it2struve0(x, out=None) = <ufunc 'it2struve0'>#
Integral related to the Struve function of order 0.
Returns the integral,
\[\int_x^\infty \frac{H_0(t)}{t}\,dt\]where \(H_0\) is the Struve function of order 0.
- Parameters:
- xarray_like
Lower limit of integration.
- outndarray, optional
Optional output array for the function values
- Returns:
- Iscalar or ndarray
The value of the integral.
See also
Notes
Wrapper for a Fortran routine created by Shanjie Zhang and Jianming Jin [1].
References
[1]Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996. https://people.sc.fsu.edu/~jburkardt/f_src/special_functions/special_functions.html
Examples
Evaluate the function at one point.
>>> import numpy as np >>> from scipy.special import it2struve0 >>> it2struve0(1.) 0.9571973506383524
Evaluate the function at several points by supplying an array for x.
>>> points = np.array([1., 2., 3.5]) >>> it2struve0(points) array([0.95719735, 0.46909296, 0.10366042])
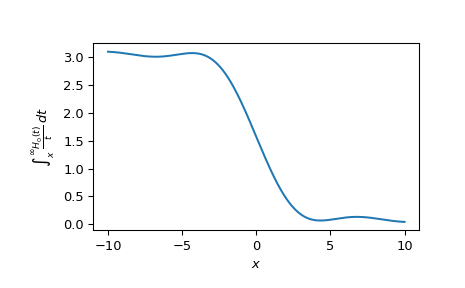
Plot the function from -10 to 10.
>>> import matplotlib.pyplot as plt >>> x = np.linspace(-10., 10., 1000) >>> it2struve0_values = it2struve0(x) >>> fig, ax = plt.subplots() >>> ax.plot(x, it2struve0_values) >>> ax.set_xlabel(r'$x$') >>> ax.set_ylabel(r'$\int_x^{\infty}\frac{H_0(t)}{t}\,dt$') >>> plt.show()