Smoothing splines#
Spline smoothing in 1D#
For the interpolation problem, the task is to construct a curve which passes through a given set of data points. This may be not appropriate if the data is noisy: we then want to construct a smooth curve, \(g(x)\), which approximates input data without passing through each point exactly.
To this end, scipy.interpolate allows constructing smoothing splines which
balance how close the resulting curve, \(g(x)\), is to the data, and
the smoothness of \(g(x)\). Mathematically, the task is to solve
a penalized least-squares problem, where the penalty controls the smoothness of
\(g(x)\).
We provide two approaches to constructing smoothing splines, which differ in (1) the form of the penalty term, and (2) the basis in which the smoothing curve is constructed. Below we consider these two approaches.
The former variant is performed by the make_smoothing_spline function,
which is a clean-room reimplementation of the classic gcvspl Fortran package
by H. Woltring.
The latter variant is implemented by the make_splrep function, which is a
reimplementation of the Fortran FITPACK library by P. Dierckx. A legacy interface
to the FITPACK library is also available.
“Classic” smoothing splines and generalized cross-validation (GCV) criterion#
Given the data arrays x and y and the array of
non-negative weights, w, we look for a cubic spline function g(x)
which minimizes
where \(\lambda \geqslant 0\) is a non-negative penalty parameter, and \(g^{(2)}(x)\) is the second derivative of \(g(x)\). The summation in the first term runs over the data points, \((x_j, y_j)\), and the integral in the second term is over the whole interval \(x \in [x_1, x_n]\).
Here the first term penalizes the deviation of the spline function from the data, and the second term penalizes large values of the second derivative—which is taken as the criterion for the smoothness of a curve.
The target function, \(g(x)\), is taken to be a natural cubic spline with knots at the data points, \(x_j\), and the minimization is carried over the spline coefficients at a given value of \(\lambda\).
Clearly, \(\lambda = 0\) corresponds to the interpolation problem—the result is a natural interpolating spline; in the opposite limit, \(\lambda \gg 1\), the result \(g(x)\) approaches a straight line (since the minimization effectively zeros out the second derivative of \(g(x)\)).
The smoothing function strongly depends on \(\lambda\), and multiple strategies are possible for selecting an “optimal” value of the penalty. One popular strategy is the so-called generalized cross-validation (GCV): conceptually, this is equivalent to comparing the spline functions constructed on reduced sets of data where we leave out one data point. Direct application of this leave-one-out cross-validation procedure is very costly, and we use a more efficient GCV algorithm.
To construct the smoothing spline given data and the penalty parameter,
we use the function make_smoothing_spline. Its interface is similar to the
constructor of interpolating splines, make_interp_spline: it accepts data arrays
and returns a callable BSpline instance.
Additionally, it accepts an optional lam keyword argument to specify the penalty
parameter \(\lambda\). If omitted or set to None, \(\lambda\) is computed
via the GCV procedure.
To illustrate the effect of the penalty parameter, consider a toy example of a sine curve with some noise:
>>> import numpy as np
>>> from scipy.interpolate import make_smoothing_spline
Generate some noisy data:
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Construct and plot smoothing splines for a series of values of the penalty parameter:
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> for lam in [0, 0.02, 10, None]:
... spl = make_smoothing_spline(x, y, lam=lam)
... plt.plot(xnew, spl(xnew), '-.', label=fr'$\lambda=${lam}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
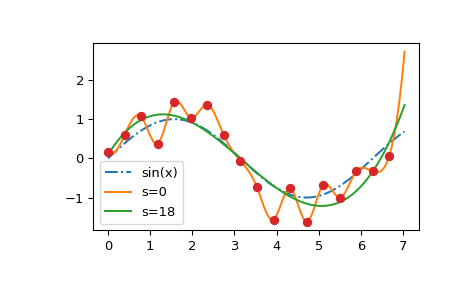
We clearly see that lam=0 constructs the interpolating spline; large values
of lam flatten out the resulting curve towards a straight line; and the GCV
result, lam=None, is close to the underlying sine curve.
Batching of y arrays#
make_smoothing_spline constructor accepts multidimensional y arrays and an
optional axis parameter and interprets them exactly the same way the
interpolating spline constructor, make_interp_spline does. See the
interpolation section for a discussion and
examples.
Smoothing splines with automatic knot selection#
As an addition to make_smoothing_spline, SciPy provides an alternative, in the
form of make_splrep and make_splprep routines. The former constructs spline
functions and the latter is for parametric spline curves in \(d > 1\) dimensions.
While having a similar API (receive the data arrays, return a BSpline instance),
these differ from make_smoothing_spline in several ways:
the functional form of the penalty term is different: these routines use jumps of the \(k\)-th derivative instead of the integral of the \((k-1)\)-th derivative;
instead of the penalty parameter \(\lambda\), a smoothness parameter \(s\) is used;
these routines automatically construct the knot vector; depending on inputs, resulting splines may have much fewer knots than data points.
by default boundary conditions differ: while
make_smoothing_splineconstructs natural cubic splines, these routines use the not-a-knot boundary conditions by default.
Let us consider the algorithm in more detail. First, the smoothing criterion. Given a cubic spline function, \(g(x)\), defined by the knots, \(t_j\), and coefficients, \(c_j\), consider the jumps of the third derivative at internal knots,
(For degree-\(k\) splines, we would have used jumps of the \(k\)-th derivative.)
If all \(D_j = 0\), then \(g(x)\) is a single polynomial on the whole domain spanned by the knots. We thus consider \(g(x)\) to be a piecewise \(C^2\)-differentiable spline function and use as the smoothing criterion the sum of jumps,
where the minimization performed is over the spline coefficients, and, potentially, the spline knots.
To make sure \(g(x)\) approximates the input data, \(x_j\) and \(y_j\), we introduce the smoothness parameter \(s \geqslant 0\) and add a constraint that
In this formulation, the smoothness parameter \(s\) is a user input, much like the penalty parameter \(\lambda\) is for the classic smoothing splines.
Note that the limit s = 0 corresponds to the interpolation problem where
\(g(x_j) = y_j\). Increasing s leads to smoother fits, and in the limit
of a very large s, \(g(x)\) degenerates into a single best-fit polynomial.
For a fixed knot vector and a given value of \(s\), the minimization problem is linear. If we also minimize with respect to the knots, the problem becomes non-linear. We thus need to specify an iterative minimization process to construct the knot vector along with the spline coefficients.
We therefore use the following procedure:
we start with a spline with no internal knots, and check the smoothness condition for the user-provided value of \(s\). If it is satisfied, we are done. Otherwise,
iterate, where on each iteration we
add new knots by splitting the interval with the maximum deviation between the spline function \(g(x_j)\) and the data \(y_j\).
construct the next approximation for \(g(x)\) and check the smoothness criterion.
The iterations stop if either the smoothness condition is satisfied, or the
maximum allowed number of knots is reached. The latter can be either specified
by a user, or is taken as the default value len(x) + k + 1 which corresponds
to the interpolation of the data array x with splines of degree k.
Rephrasing and glossing over details, the procedure is to iterate over the
knot vectors generated by generate_knots, applying make_lsq_spline on each
step. In pseudocode:
for t in generate_knots(x, y, s=s):
g = make_lsq_spline(x, y, t=t) # construct
if ((y - g(x))**2).sum() < s: # check smoothness
break
Note
For s=0, we take a short-cut and construct the interpolating spline
with the not-a-knot boundary condition instead of iterating.
The iterative procedure of constructing a knot vector is available through the
generator function generate_knots. To illustrate:
>>> import numpy as np
>>> from scipy.interpolate import generate_knots
>>> x = np.arange(7)
>>> y = x**4
>>> list(generate_knots(x, y, s=1)) # default is cubic splines, k=3
[array([0., 0., 0., 0., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 3., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 3., 5., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.])]
For s=0, the generator cuts short:
>>> list(generate_knots(x, y, s=0))
[array([0, 0, 0, 0, 2, 3, 4, 6, 6, 6, 6])]
Note
In general, knots are placed at data sites. The exception is even-order
splines, where the knots can be placed away from data. This happens when
s=0 (interpolation), or when s is small enough so that the maximum number
of knots is reached, and the routine switches to the s=0 knot vector
(sometimes known as Greville abscissae).
>>> list(generate_knots(x, y, s=1, k=2)) # k=2, quadratic spline
[array([0., 0., 0., 6., 6., 6.]),
array([0., 0., 0., 3., 6., 6., 6.]),
array([0., 0., 0., 3., 5., 6., 6., 6.]),
array([0., 0., 0., 2., 3., 5., 6., 6., 6.]),
array([0. , 0. , 0. , 1.5, 2.5, 3.5, 4.5, 6. , 6. , 6. ])] # Greville sites
Note
The heuristics for constructing the knot vector follows the algorithm used by the FITPACK Fortran library. The algorithm is the same, and small differences are possible due to floating-point rounding.
We now illustrate make_splrep results, using the same toy dataset as in the previous section
>>> import numpy as np
>>> from scipy.interpolate import make_splrep
Generate some noisy data
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Construct and plot smoothing splines for a series of values of the s
parameter:
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, make_splrep(x, y, s=0)(xnew), '-', label='s=0')
>>> plt.plot(xnew, make_splrep(x, y, s=len(x))(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
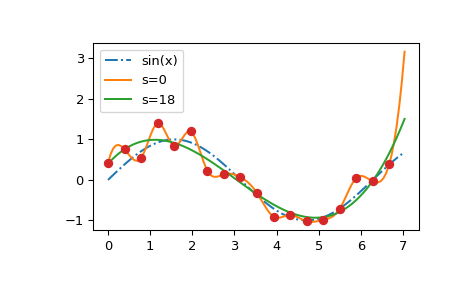
We see that the \(s=0\) curve follows the (random) fluctuations of the data points, while the \(s > 0\) curve is close to the underlying sine function. Also note that the extrapolated values vary wildly depending on the value of \(s\).
Finding a good value of \(s\) is a trial-and-error process. If the weights correspond to the inverse of standard deviations of the input data, a “good” value of \(s\) is expected to be somewhere between \(m - \sqrt{2m}\) and \(m + \sqrt{2m}\), where \(m\) is the number of data points. If all weights equal unity, a reasonable choice might be around \(s \sim m\,\sigma^2\), where \(\sigma\) is an estimate for the standard deviation of the data.
Note
The number of knots a very strongly dependent on s. It is possible that
small variations of s lead to drastic changes in the knot number.
Note
Both make_smoothing_spline and make_splrep allow for weighted fits,
where the user provides an array of weights, w. Note that the definition
differs somewhat: make_smoothing_spline squares the weights to be consistent
with gcvspl, while make_splrep does not—to be consistent with FITPACK.
Smoothing spline curves in \(d>1\)#
So far we considered constructing smoothing spline functions, \(g(x)\) given
data arrays x and y. We now consider a related problem of constructing
a smoothing spline curve, where we consider the data as points on a plane,
\(\mathbf{p}_j = (x_j, y_j)\), and we want to construct a parametric function
\(\mathbf{g}(\mathbf{p}) = (g_x(u), g_y(u))\), where the values of the
parameter \(u_j\) correspond to \(x_j\) and \(y_j\).
Note that this problem readily generalizes to higher dimensions, \(d > 2\): we simply have \(d\) data arrays and construct a parametric function with \(d\) components.
Also note that the choice of parametrization cannot be automated, and different parameterizations can lead to very different curves for the same data, even for interpolating curves.
Once a specific form of parametrization is chosen, the problem of constructing a smoothing curve is conceptually very similar to constructing a smoothing spline function. In a nutshell,
spline knots are added from the values of the parameter \(u\), and
both the cost function to minimize and the constraint we considered for spline functions simply get an extra summation over the \(d\) components.
The “parametric” generalization of the make_splrep function is make_splprep,
and its docstring spells out the precise mathematical formulation of the minimization
problem it solves.
The main user-visible difference of the parametric case is the user interface:
instead of two data arrays,
xandy,make_splprepreceives a single two-dimensional array, where the first dimension has size \(d\) and each data array is stored along the second dimension (alternatively, you can supply a list of 1D arrays).the return value is pair: a
BSplineinstance and the array of parameter values,u, which corresponds to the input data arrays.
By default, make_splprep constructs and returns the cord length parametrization
of input data (see the Parametric spline curves
section for details). Alternatively, you can provide your own array of
parameter values, u.
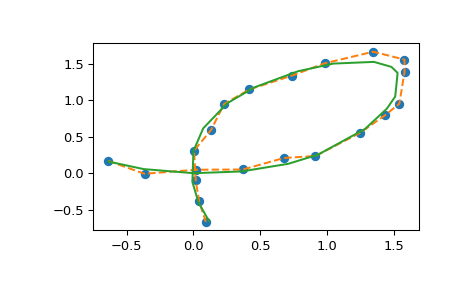
To illustrate the API, consider a toy problem: we have some data sampled from a folium of Descartes plus some noise.
>>> import numpy as np
>>> from scipy.interpolate import make_splprep
>>> th = np.linspace(-0.2, np.pi/2 + 0.2, 21)
>>> r = 3 * np.sin(th) * np.cos(th) / (np.sin(th)**3 + np.cos(th)**3)
>>> x, y = r * np.cos(th), r * np.sin(th)
Add some noise and construct the interpolators
>>> rng = np.random.default_rng()
>>> xn = x + 0.1*rng.uniform(-1, 1, size=len(x))
>>> yn = y + 0.1*rng.uniform(-1, 1, size=len(x))
>>> spl, u = make_splprep([xn, yn], s=0) # note the [xn, yn] argument
>>> spl_n, u_n = make_splprep([xn, yn], s=0.1)
And plot the results (the result of spl(u) is a 2D array, so we unpack it
into a pair of x and y arrays for plotting).
>>> import matplotlib.pyplot as plt
>>> plt.plot(xn, yn, 'o')
>>> plt.plot(*spl(u), '--')
>>> plt.plot(*spl_n(u_n), '-')
>>> plt.show()
Batching of y arrays#
Unlike interpolating splines and
GCV smoothers, make_splrep and make_splprep
do not allow multidimensional y arrays and require that x.ndim == y.ndim == 1.
The technical reason for this limitation is that the length of the knot vector t
depends on the y values, thus for a batched y, the batched t could be a
ragged array, which BSpline is not equipped to handle.
Therefore if you need to handle batched inputs, you will need to loop over the
batch manually and construct a BSpline object per slice of the batch.
Having done that, you can mimic BSpline behavior for evaluations with a workaround
along the lines of
class BatchSpline:
"""BSpline-like class with batch behavior."""
def __init__(self, x, y, axis, *, spline, **kwargs):
y = np.moveaxis(y, axis, -1)
self._batch_shape = y.shape[:-1]
self._splines = [
spline(x, yi, **kwargs) for yi in y.reshape(-1, y.shape[-1])
]
self._axis = axis
def __call__(self, x):
y = [spline(x) for spline in self._splines]
y = np.reshape(y, self._batch_shape + x.shape)
return np.moveaxis(y, -1, self._axis) if x.shape else y
Legacy routines for spline smoothing in 1-D#
In addition to smoothing splines constructors we discussed in the previous sections,
scipy.interpolate provides direct interfaces for routines from the venerable FITPACK
Fortran library authored by P. Dierckx.
Note
These interfaces should be considered legacy—while we do not
plan to deprecate or remove them, we recommend that new code uses more modern
alternatives, make_smoothing_spline, make_splrep or make_splprep, instead.
For historical reasons, scipy.interpolate provides two equivalent interfaces
for FITPACK, a interface and an object-oriented interface. While equivalent, these interfaces
have different defaults. Below we discuss them in turn, starting from the
functional interface.
Procedural (splrep)#
Spline interpolation requires two essential steps: (1) a spline
representation of the curve is computed, and (2) the spline is
evaluated at the desired points. In order to find the spline
representation, there are two different ways to represent a curve and
obtain (smoothing) spline coefficients: directly and parametrically.
The direct method finds the spline representation of a curve in a 2-D
plane using the function splrep. The
first two arguments are the only ones required, and these provide the
\(x\) and \(y\) components of the curve. The normal output is
a 3-tuple, \(\left(t,c,k\right)\) , containing the knot-points,
\(t\) , the coefficients \(c\) and the order \(k\) of the
spline. The default spline order is cubic, but this can be changed
with the input keyword, k.
The knot array defines the interpolation interval to be t[k:-k], so that
the first \(k+1\) and last \(k+1\) entries of the t array define
boundary knots. The coefficients are a 1D array of length at least
len(t) - k - 1. Some routines pad this array to have len(c) == len(t)—
these additional coefficients are ignored for the spline evaluation.
The tck-tuple format is compatible with
interpolating b-splines: the output of
splrep can be wrapped into a BSpline object, e.g. BSpline(*tck), and
the evaluation/integration/root-finding routines described below
can use tck-tuples and BSpline objects interchangeably.
For curves in N-D space the function
splprep allows defining the curve
parametrically. For this function only 1 input argument is
required. This input is a list of \(N\) arrays representing the
curve in N-D space. The length of each array is the
number of curve points, and each array provides one component of the
N-D data point. The parameter variable is given
with the keyword argument, u, which defaults to an equally-spaced
monotonic sequence between \(0\) and \(1\) (i.e., the uniform
parametrization).
The output consists of two objects: a 3-tuple, \(\left(t,c,k\right)\) , containing the spline representation and the parameter variable \(u.\)
The coefficients are a list of \(N\) arrays, where each array corresponds to
a dimension of the input data. Note that the knots, t correspond to the
parametrization of the curve u.
The keyword argument, s , is used to specify the amount of smoothing
to perform during the spline fit. The default value of \(s\) is
\(s=m-\sqrt{2m}\) where \(m\) is the number of data points
being fit. Therefore, if no smoothing is desired a value of
\(\mathbf{s}=0\) should be passed to the routines.
Once the spline representation of the data has been determined, it can be
evaluated either using the splev function or by wrapping
the tck tuple into a BSpline object, as demonstrated below.
We start by illustrating the effect of the s parameter on smoothing some
synthetic noisy data
>>> import numpy as np
>>> from scipy.interpolate import splrep, BSpline
Generate some noisy data
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Construct two splines with different values of s.
>>> tck = splrep(x, y, s=0)
>>> tck_s = splrep(x, y, s=len(x))
And plot them
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, BSpline(*tck)(xnew), '-', label='s=0')
>>> plt.plot(xnew, BSpline(*tck_s)(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
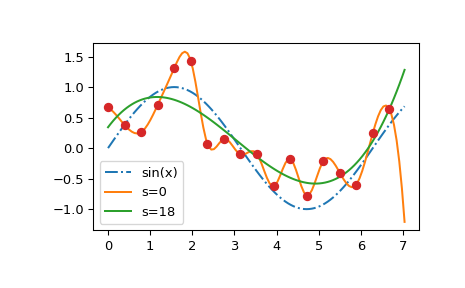
We see that the s=0 curve follows the (random) fluctuations of the data points,
while the s > 0 curve is close to the underlying sine function.
Also note that the extrapolated values vary wildly depending on the value of s.
The default value of s depends on whether the weights are supplied or not,
and also differs for splrep and splprep. Therefore, we recommend always
providing the value of s explicitly.
Manipulating spline objects: procedural (splXXX)#
Once the spline representation of the data has been determined,
functions are available for evaluating the spline
(splev) and its derivatives
(splev, spalde) at any point
and the integral of the spline between any two points (
splint). In addition, for cubic splines ( \(k=3\)
) with 8 or more knots, the roots of the spline can be estimated (
sproot). These functions are demonstrated in the
example that follows.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
Cubic spline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = interpolate.splev(xnew, tck, der=0)
Note that the last line is equivalent to BSpline(*tck)(xnew).
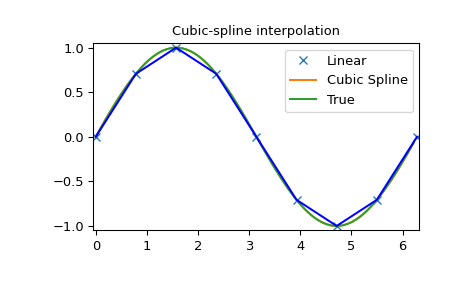
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Cubic-spline interpolation')
>>> plt.show()
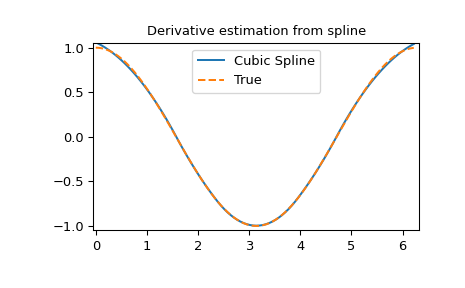
Derivative of spline
>>> yder = interpolate.splev(xnew, tck, der=1) # or BSpline(*tck)(xnew, 1)
>>> plt.figure()
>>> plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Derivative estimation from spline')
>>> plt.show()
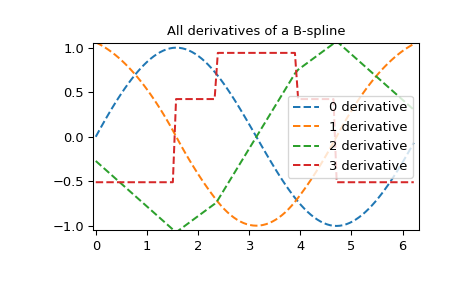
All derivatives of spline
>>> yders = interpolate.spalde(xnew, tck)
>>> plt.figure()
>>> for i in range(len(yders[0])):
... plt.plot(xnew, [d[i] for d in yders], '--', label=f"{i} derivative")
>>> plt.legend()
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('All derivatives of a B-spline')
>>> plt.show()
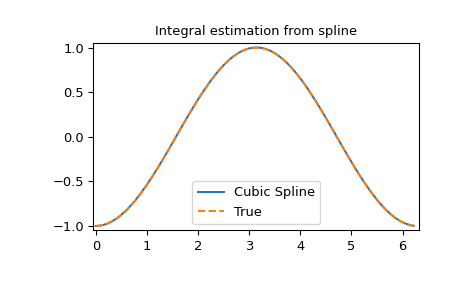
Integral of spline
>>> def integ(x, tck, constant=-1):
... x = np.atleast_1d(x)
... out = np.zeros(x.shape, dtype=x.dtype)
... for n in range(len(out)):
... out[n] = interpolate.splint(0, x[n], tck)
... out += constant
... return out
>>> yint = integ(xnew, tck)
>>> plt.figure()
>>> plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Integral estimation from spline')
>>> plt.show()
Roots of spline
>>> interpolate.sproot(tck)
array([3.1416]) # may vary
Notice that sproot may fail to find an obvious solution at the edge of the
approximation interval, \(x = 0\). If we define the spline on a slightly
larger interval, we recover both roots \(x = 0\) and \(x = \pi\):
>>> x = np.linspace(-np.pi/4, np.pi + np.pi/4, 51)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> interpolate.sproot(tck)
array([0., 3.1416])
Parametric spline
>>> t = np.arange(0, 1.1, .1)
>>> x = np.sin(2*np.pi*t)
>>> y = np.cos(2*np.pi*t)
>>> tck, u = interpolate.splprep([x, y], s=0)
>>> unew = np.arange(0, 1.01, 0.01)
>>> out = interpolate.splev(unew, tck)
>>> plt.figure()
>>> plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-1.05, 1.05, -1.05, 1.05])
>>> plt.title('Spline of parametrically-defined curve')
>>> plt.show()
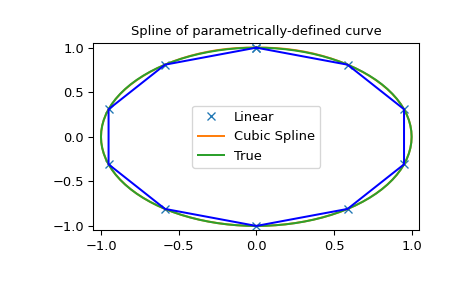
Note that in the last example, splprep returns the spline coefficients as a
list of arrays, where each array corresponds to a dimension of the input data.
Thus to wrap its output to a BSpline, we need to transpose the coefficients
(or use BSpline(..., axis=1)):
>>> tt, cc, k = tck
>>> cc = np.array(cc)
>>> bspl = BSpline(tt, cc.T, k) # note the transpose
>>> xy = bspl(u)
>>> xx, yy = xy.T # transpose to unpack into a pair of arrays
>>> np.allclose(x, xx)
True
>>> np.allclose(y, yy)
True
Object-oriented (UnivariateSpline)#
The spline-fitting capabilities described above are also available via
an objected-oriented interface. The 1-D splines are
objects of the UnivariateSpline class, and are created with the
\(x\) and \(y\) components of the curve provided as arguments
to the constructor. The class defines __call__, allowing the object
to be called with the x-axis values, at which the spline should be
evaluated, returning the interpolated y-values. This is shown in
the example below for the subclass InterpolatedUnivariateSpline.
The integral,
derivatives, and
roots methods are also available
on UnivariateSpline objects, allowing definite integrals,
derivatives, and roots to be computed for the spline.
The UnivariateSpline class can also be used to smooth data by
providing a non-zero value of the smoothing parameter s, with the
same meaning as the s keyword of the splrep function
described above. This results in a spline that has fewer knots
than the number of data points, and hence is no longer strictly
an interpolating spline, but rather a smoothing spline. If this
is not desired, the InterpolatedUnivariateSpline class is available.
It is a subclass of UnivariateSpline that always passes through all
points (equivalent to forcing the smoothing parameter to 0). This
class is demonstrated in the example below.
The LSQUnivariateSpline class is the other subclass of UnivariateSpline.
It allows the user to specify the number and location of internal
knots explicitly with the parameter t. This allows for the creation
of customized splines with non-linear spacing, to interpolate in
some domains and smooth in others, or change the character of the
spline.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
InterpolatedUnivariateSpline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> s = interpolate.InterpolatedUnivariateSpline(x, y)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('InterpolatedUnivariateSpline')
>>> plt.show()

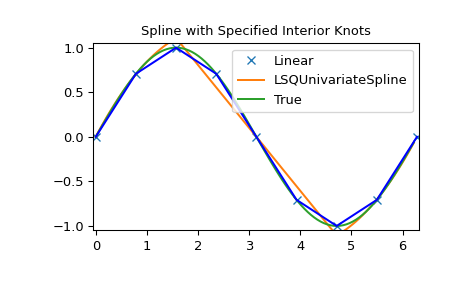
LSQUnivarateSpline with non-uniform knots
>>> t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
>>> s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Spline with Specified Interior Knots')
>>> plt.show()
2-D smoothing splines#
In addition to smoothing 1-D splines, the FITPACK library provides the means of fitting 2-D surfaces to two-dimensional data. The surfaces can be thought of as functions of two arguments, \(z = g(x, y)\), constructed as tensor products of 1-D splines.
Assuming that the data is held in three arrays, x, y and z,
there are two ways these data arrays can be interpreted. First—the scattered
interpolation problem—the data is assumed to be paired, i.e. the pairs of
values x[i] and y[i] represent the coordinates of the point i, which
corresponds to z[i].
The surface \(g(x, y)\) is constructed to satisfy
where \(w_i\) are non-negative weights, and s is the input parameter,
known as the smoothing factor, which controls the interplay between smoothness
of the resulting function g(x, y) and the quality of the approximation of
the data (i.e., the differences between \(g(x_i, y_i)\) and \(z_i\)). The
limit of \(s = 0\) formally corresponds to interpolation, where the surface
passes through the input data, \(g(x_i, y_i) = z_i\). See the note below however.
The second case—the rectangular grid interpolation problem—is where the data
points are assumed to be on a rectangular grid defined by all pairs of the
elements of the x and y arrays. For this problem, the z array is
assumed to be two-dimensional, and z[i, j] corresponds to (x[i], y[j]).
The bivariate spline function \(g(x, y)\) is constructed to satisfy
where s is the smoothing factor. Here the limit of \(s=0\) also
formally corresponds to interpolation, \(g(x_i, y_j) = z_{i, j}\).
Note
Internally, the smoothing surface \(g(x, y)\) is constructed by placing spline knots into the bounding box defined by the data arrays. The knots are placed automatically via the FITPACK algorithm until the desired smoothness is reached.
The knots may be placed away from the data points.
While \(s=0\) formally corresponds to a bivariate spline interpolation, the FITPACK algorithm is not meant for interpolation, and may lead to unexpected results.
For scattered data interpolation, prefer griddata; for data on a regular
grid, prefer RegularGridInterpolator.
Note
If the input data, x and y, is such that input dimensions
have incommensurate units and differ by many orders of magnitude, the
interpolant \(g(x, y)\) may have numerical artifacts. Consider
rescaling the data before interpolation.
We now consider the two spline fitting problems in turn.
Bivariate spline fitting of scattered data#
There are two interfaces for the underlying FITPACK library, a procedural one and an object-oriented interface.
Procedural interface (`bisplrep`)
For (smooth) spline fitting to a 2-D surface, the function
bisplrep is available. This function takes as required inputs
the 1-D arrays x, y, and z, which represent points on the
surface \(z=f(x, y).\) The spline orders in x and y directions can
be specified via the optional parameters kx and ky. The default is
a bicubic spline, kx=ky=3.
The output of bisplrep is a list [tx ,ty, c, kx, ky] whose entries represent
respectively, the components of the knot positions, the coefficients
of the spline, and the order of the spline in each coordinate. It is
convenient to hold this list in a single object, tck, so that it can
be passed easily to the function bisplev. The
keyword, s , can be used to change the amount of smoothing performed
on the data while determining the appropriate spline. The recommended values
for \(s\) depend on the weights \(w_i\). If these are taken as \(1/d_i\),
with \(d_i\) an estimate of the standard deviation of \(z_i\), a
good value of \(s\) should be found in the range \(m- \sqrt{2m}, m +
\sqrt{2m}\), where where \(m\) is the number of data points in the x,
y, and z vectors.
The default value is \(s=m-\sqrt{2m}\). As a result, if no smoothing is desired, then ``s=0`` should be passed to `bisplrep`. (See however the note above).
To evaluate the 2-D spline and its partial derivatives
(up to the order of the spline), the function
bisplev is required. This function takes as the
first two arguments two 1-D arrays whose cross-product specifies
the domain over which to evaluate the spline. The third argument is
the tck list returned from bisplrep. If desired,
the fourth and fifth arguments provide the orders of the partial
derivative in the \(x\) and \(y\) direction, respectively.
Note
It is important to note that 2-D interpolation should not
be used to find the spline representation of images. The algorithm
used is not amenable to large numbers of input points. scipy.signal
and scipy.ndimage contain more appropriate algorithms for finding
the spline representation of an image.
The 2-D interpolation commands are intended for use when interpolating a 2-D
function as shown in the example that follows. This
example uses the mgrid command in NumPy which is
useful for defining a “mesh-grid” in many dimensions. (See also the
ogrid command if the full-mesh is not
needed). The number of output arguments and the number of dimensions
of each argument is determined by the number of indexing objects
passed in mgrid.
>>> import numpy as np
>>> from scipy import interpolate
>>> import matplotlib.pyplot as plt
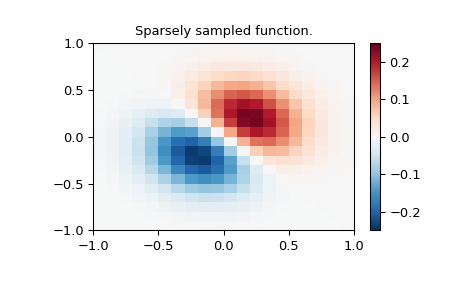
Define function over a sparse 20x20 grid
>>> x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
>>> x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
>>> y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
>>> z = (x+y) * np.exp(-6.0*(x*x+y*y))
>>> plt.figure()
>>> lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
>>> plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Sparsely sampled function.")
>>> plt.show()
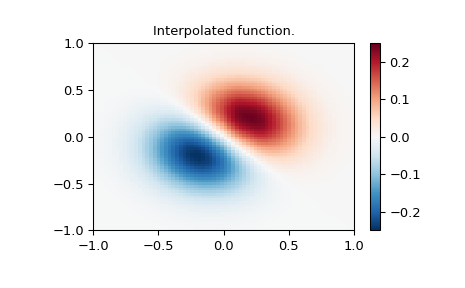
Interpolate function over a new 70x70 grid
>>> xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
>>> xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
>>> ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
>>> tck = interpolate.bisplrep(x, y, z, s=0)
>>> znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)
>>> plt.figure()
>>> plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Interpolated function.")
>>> plt.show()
Object-oriented interface (`SmoothBivariateSpline`)
The object-oriented interface for bivariate spline smoothing of scattered data,
SmoothBivariateSpline class, implements a subset of the functionality of the
bisplrep / bisplev pair, and has different defaults.
It takes the elements of the weights array equal unity, \(w_i = 1\) and constructs the knot vectors automatically given the input value of the smoothing factor s— the default value is \(m\), the number of data points.
The spline orders in the x and y directions are controlled by the optional
parameters kx and ky, with the default of kx=ky=3.
We illustrate the effect of the smoothing factor using the following example:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import SmoothBivariateSpline
import warnings
warnings.simplefilter('ignore')
train_x, train_y = np.meshgrid(np.arange(-5, 5, 0.5), np.arange(-5, 5, 0.5))
train_x = train_x.flatten()
train_y = train_y.flatten()
def z_func(x, y):
return np.cos(x) + np.sin(y) ** 2 + 0.05 * x + 0.1 * y
train_z = z_func(train_x, train_y)
interp_func = SmoothBivariateSpline(train_x, train_y, train_z, s=0.0)
smth_func = SmoothBivariateSpline(train_x, train_y, train_z)
test_x = np.arange(-9, 9, 0.01)
test_y = np.arange(-9, 9, 0.01)
grid_x, grid_y = np.meshgrid(test_x, test_y)
interp_result = interp_func(test_x, test_y).T
smth_result = smth_func(test_x, test_y).T
perfect_result = z_func(grid_x, grid_y)
fig, axes = plt.subplots(1, 3, figsize=(16, 8))
extent = [test_x[0], test_x[-1], test_y[0], test_y[-1]]
opts = dict(aspect='equal', cmap='nipy_spectral', extent=extent, vmin=-1.5, vmax=2.5)
im = axes[0].imshow(perfect_result, **opts)
fig.colorbar(im, ax=axes[0], orientation='horizontal')
axes[0].plot(train_x, train_y, 'w.')
axes[0].set_title('Perfect result, sampled function', fontsize=21)
im = axes[1].imshow(smth_result, **opts)
axes[1].plot(train_x, train_y, 'w.')
fig.colorbar(im, ax=axes[1], orientation='horizontal')
axes[1].set_title('s=default', fontsize=21)
im = axes[2].imshow(interp_result, **opts)
fig.colorbar(im, ax=axes[2], orientation='horizontal')
axes[2].plot(train_x, train_y, 'w.')
axes[2].set_title('s=0', fontsize=21)
plt.tight_layout()
plt.show()
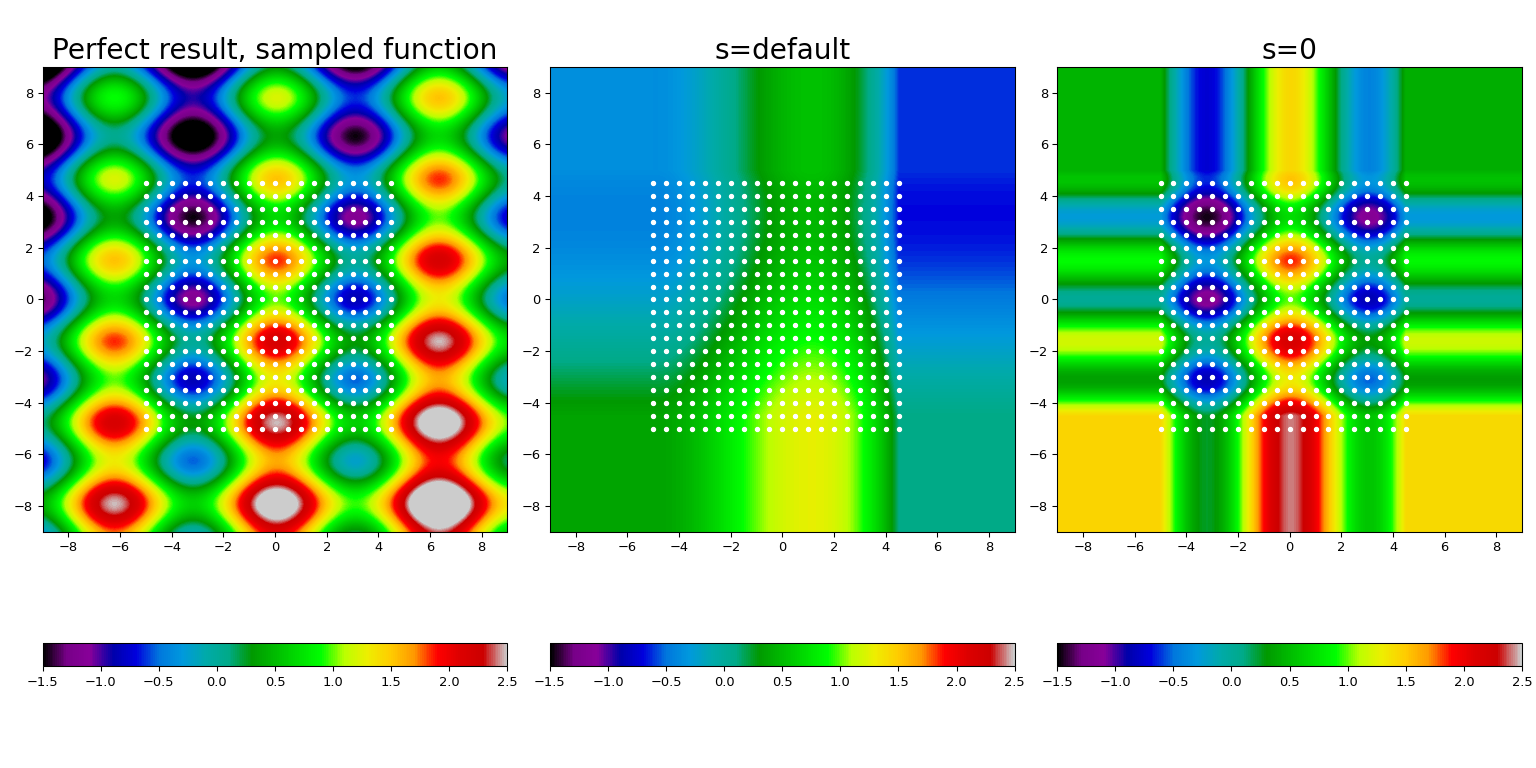
Here we take a known function (displayed at the leftmost panel), sample it on a mesh of points (shown by white dots), and construct the spline fit using the default smoothing (center panel) and forcing the interpolation (rightmost panel).
Several features are clearly visible. First, the default value of s provides
too much smoothing for this data; forcing the interpolation condition, s = 0,
allows to restore the underlying function to a reasonable accuracy. Second,
outside of the interpolation range (i.e., the area covered by
white dots) the result is extrapolated using a nearest-neighbor constant.
Finally, we had to silence the warnings (which is a bad form, yes!).
The warning here is emitted in the s=0 case, and signals an internal difficulty
FITPACK encountered when we forced the interpolation condition. If you see
this warning in your code, consider switching to bisplrep and increase its
nxest, nyest parameters (see the bisplrep docstring for more details).
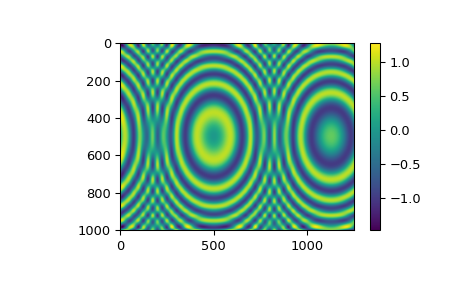
Bivariate spline fitting of data on a grid#
For gridded 2D data, fitting a smoothing tensor product spline can be done
using the RectBivariateSpline class. It has the interface similar to that of
SmoothBivariateSpline, the main difference is that the 1D input arrays x
and y are understood as defining a 2D grid (as their outer product),
and the z array is 2D with the shape of len(x) by len(y).
The spline orders in the x and y directions are controlled by the optional
parameters kx and ky, with the default of kx=ky=3, i.e. a bicubic
spline.
The default value of the smoothing factor is s=0. We nevertheless recommend
to always specify s explicitly.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline
x = np.arange(-5.01, 5.01, 0.25) # the grid is an outer product
y = np.arange(-5.01, 7.51, 0.25) # of x and y arrays
xx, yy = np.meshgrid(x, y, indexing='ij')
z = np.sin(xx**2 + 2.*yy**2) # z array needs to be 2-D
func = RectBivariateSpline(x, y, z, s=0)
xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 7.51, 1e-2)
znew = func(xnew, ynew)
plt.imshow(znew)
plt.colorbar()
plt.show()
Bivariate spline fitting of data in spherical coordinates#
If your data is given in spherical coordinates, \(r = r(\theta, \phi)\),
SmoothSphereBivariateSpline and RectSphereBivariateSpline provide convenient
analogs of SmoothBivariateSpline and RectBivariateSpline, respectively.
These classes ensure the periodicity of the spline fits for \(\theta \in [0, \pi]\) and \(\phi \in [0, 2\pi]\), and offer some control over the continuity at the poles. Refer to the docstrings of these classes for details.