Fourier Transforms (scipy.fft)#
Fourier analysis is a method for expressing a function as a sum of periodic components, and for recovering the signal from those components. When both the function and its Fourier transform are replaced with discretized counterparts, it is called the discrete Fourier transform (DFT). The DFT has become a mainstay of numerical computing in part because of a very fast algorithm for computing it, called the Fast Fourier Transform (FFT), which was known to Gauss (1805) and was brought to light in its current form by Cooley and Tukey [CT65]. Press et al. [NR07] provide an accessible introduction to Fourier analysis and its applications.
Fast Fourier transforms#
1-D discrete Fourier transforms#
The FFT y[k] of length \(N\) of the length-\(N\) sequence x[n] is
defined as
and the inverse transform is defined as follows
These transforms can be calculated by means of fft and ifft,
respectively, as shown in the following example.
>>> from scipy.fft import fft, ifft
>>> import numpy as np
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> y = fft(x)
>>> y
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yinv = ifft(y)
>>> yinv
array([ 1.0+0.j, 2.0+0.j, 1.0+0.j, -1.0+0.j, 1.5+0.j])
From the definition of the FFT it can be seen that
In the example
>>> np.sum(x)
4.5
which corresponds to \(y[0]\). For N even, the elements \(y[1], ..., y[N/2-1]\) contain the positive-frequency terms, and the elements \(y[N/2], ..., y[N-1]\) contain the negative-frequency terms, in order of decreasingly negative frequency. For N odd, the elements \(y[1], ..., y[(N-1)/2]\) contain the positive-frequency terms, and the elements \(y[(N+1)/2], ..., y[N-1]\) contain the negative-frequency terms, in order of decreasingly negative frequency.
In case the sequence x is real-valued, the values of \(y[n]\) for positive frequencies is the conjugate of the values \(y[n]\) for negative frequencies (because the spectrum is symmetric). Typically, only the FFT corresponding to positive frequencies is plotted.
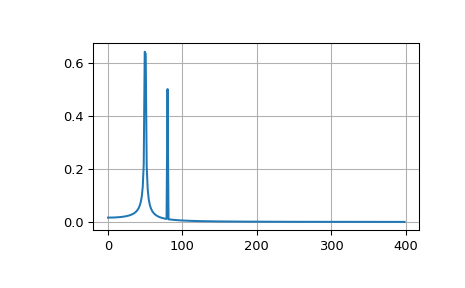
The example plots the FFT of the sum of two sines.
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
>>> plt.grid()
>>> plt.show()
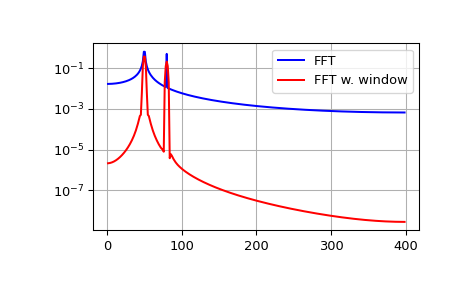
The FFT input signal is inherently truncated. This truncation can be modeled
as multiplication of an infinite signal with a rectangular window function. In
the spectral domain this multiplication becomes convolution of the signal
spectrum with the window function spectrum, being of form \(\sin(x)/x\).
This convolution is the cause of an effect called spectral leakage (see
[WPW]). Windowing the signal with a dedicated window function helps mitigate
spectral leakage. The example below uses a Blackman window from
scipy.signal and shows the effect of windowing
(the zero component of the FFT has been truncated for illustrative purposes).
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> from scipy.signal.windows import blackman
>>> w = blackman(N)
>>> ywf = fft(y*w)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(ywf[1:N//2]), '-r')
>>> plt.legend(['FFT', 'FFT w. window'])
>>> plt.grid()
>>> plt.show()
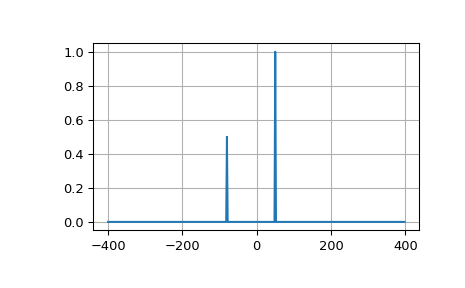
In case the sequence x is complex-valued, the spectrum is no longer symmetric. To simplify working with the FFT functions, scipy provides the following two helper functions.
The function fftfreq returns the FFT sample frequency points.
>>> from scipy.fft import fftfreq
>>> freq = fftfreq(8, 0.125)
>>> freq
array([ 0., 1., 2., 3., -4., -3., -2., -1.])
In a similar spirit, the function fftshift allows swapping the lower
and upper halves of a vector, so that it becomes suitable for display.
>>> from scipy.fft import fftshift
>>> x = np.arange(8)
>>> fftshift(x)
array([4, 5, 6, 7, 0, 1, 2, 3])
The example below plots the FFT of two complex exponentials; note the asymmetric spectrum.
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import numpy as np
>>> # number of signal points
>>> N = 400
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.exp(50.0 * 1.j * 2.0*np.pi*x) + 0.5*np.exp(-80.0 * 1.j * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)
>>> xf = fftshift(xf)
>>> yplot = fftshift(yf)
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 1.0/N * np.abs(yplot))
>>> plt.grid()
>>> plt.show()
The function rfft calculates the FFT of a real sequence and outputs the
complex FFT coefficients \(y[n]\) for only half of the frequency range. The
remaining negative frequency components are implied by the Hermitian symmetry of
the FFT for a real input (y[n] = conj(y[-n])). In case of N being even:
\([Re(y[0]) + 0j, y[1], ..., Re(y[N/2]) + 0j]\); in case of N being odd
\([Re(y[0]) + 0j, y[1], ..., y[N/2]]\). The terms shown explicitly as
\(Re(y[k]) + 0j\) are restricted to be purely real since, by the hermitian
property, they are their own complex conjugate.
The corresponding function irfft calculates the IFFT of the FFT
coefficients with this special ordering.
>>> from scipy.fft import fft, rfft, irfft
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5, 1.0])
>>> fft(x)
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j , -2.75+1.29903811j, 2.25+0.4330127j ])
>>> yr = rfft(x)
>>> yr
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j ])
>>> irfft(yr)
array([ 1. , 2. , 1. , -1. , 1.5, 1. ])
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> fft(x)
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yr = rfft(x)
>>> yr
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j])
Notice that the rfft of odd and even length signals are of the same shape.
By default, irfft assumes the output signal should be of even length. And
so, for odd signals, it will give the wrong result:
>>> irfft(yr)
array([ 1.70788987, 2.40843925, -0.37366961, 0.75734049])
To recover the original odd-length signal, we must pass the output shape by the n parameter.
>>> irfft(yr, n=len(x))
array([ 1. , 2. , 1. , -1. , 1.5])
2- and N-D discrete Fourier transforms#
The functions fft2 and ifft2 provide 2-D FFT and
IFFT, respectively. Similarly, fftn and ifftn provide
N-D FFT, and IFFT, respectively.
For real-input signals, similarly to rfft, we have the functions
rfft2 and irfft2 for 2-D real transforms;
rfftn and irfftn for N-D real transforms.
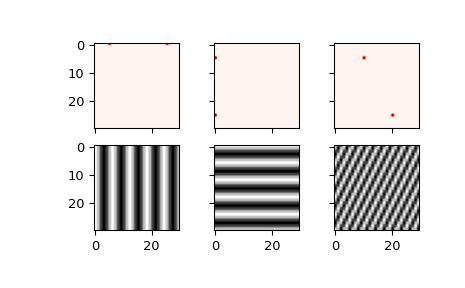
The example below demonstrates a 2-D IFFT and plots the resulting (2-D) time-domain signals.
>>> from scipy.fft import ifftn
>>> import matplotlib.pyplot as plt
>>> import matplotlib.cm as cm
>>> import numpy as np
>>> N = 30
>>> f, ((ax1, ax2, ax3), (ax4, ax5, ax6)) = plt.subplots(2, 3, sharex='col', sharey='row')
>>> xf = np.zeros((N,N))
>>> xf[0, 5] = 1
>>> xf[0, N-5] = 1
>>> Z = ifftn(xf)
>>> ax1.imshow(xf, cmap=cm.Reds)
>>> ax4.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 0] = 1
>>> xf[N-5, 0] = 1
>>> Z = ifftn(xf)
>>> ax2.imshow(xf, cmap=cm.Reds)
>>> ax5.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 10] = 1
>>> xf[N-5, N-10] = 1
>>> Z = ifftn(xf)
>>> ax3.imshow(xf, cmap=cm.Reds)
>>> ax6.imshow(np.real(Z), cmap=cm.gray)
>>> plt.show()
Discrete Cosine Transforms#
SciPy provides a DCT with the function dct and a corresponding IDCT
with the function idct. There are 8 types of the DCT [WPC], [Mak];
however, only the first 4 types are implemented in scipy. “The” DCT generally
refers to DCT type 2, and “the” Inverse DCT generally refers to DCT type 3. In
addition, the DCT coefficients can be normalized differently (for most types,
scipy provides None and ortho). Two parameters of the dct/idct
function calls allow setting the DCT type and coefficient normalization.
For a single dimension array x, dct(x, norm=’ortho’) is equal to MATLAB dct(x).
Type I DCT#
SciPy uses the following definition of the unnormalized DCT-I
(norm=None):
Note that the DCT-I is only supported for input size > 1.
Type II DCT#
SciPy uses the following definition of the unnormalized DCT-II
(norm=None):
In case of the normalized DCT (norm='ortho'), the DCT coefficients
\(y[k]\) are multiplied by a scaling factor f:
In this case, the DCT “base functions” \(\phi_k[n] = 2 f \cos \left({\pi(2n+1)k \over 2N} \right)\) become orthonormal:
Type III DCT#
SciPy uses the following definition of the unnormalized DCT-III
(norm=None):
or, for norm='ortho':
Type IV DCT#
SciPy uses the following definition of the unnormalized DCT-IV
(norm=None):
or, for norm='ortho':
DCT and IDCT#
The (unnormalized) DCT-III is the inverse of the (unnormalized) DCT-II, up to a
factor of 2N. The orthonormalized DCT-III is exactly the inverse of the
orthonormalized DCT- II. The function idct performs the mappings between
the DCT and IDCT types, as well as the correct normalization.
The following example shows the relation between DCT and IDCT for different types and normalizations.
>>> from scipy.fft import dct, idct
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
The DCT-II and DCT-III are each other’s inverses, so for an orthonormal transform we return back to the original signal.
>>> dct(dct(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
Doing the same under default normalization, however, we pick up an extra scaling factor of \(2N=10\) since the forward transform is unnormalized.
>>> dct(dct(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
For this reason, we should use the function idct using the same type for both,
giving a correctly normalized result.
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Analogous results can be seen for the DCT-I, which is its own inverse up to a factor of \(2(N-1)\).
>>> dct(dct(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-I: scaling factor 2*(N-1) = 8
>>> dct(dct(x, type=1), type=1)
array([ 8. , 16., 8. , -8. , 12.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
And for the DCT-IV, which is also its own inverse up to a factor of \(2N\).
>>> dct(dct(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-IV: scaling factor 2*N = 10
>>> dct(dct(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
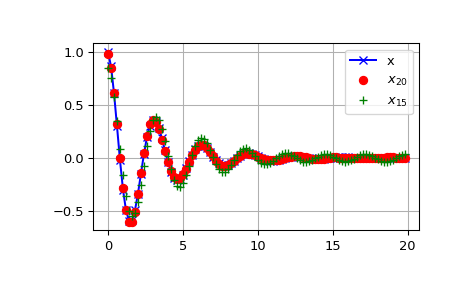
Example#
The DCT exhibits the “energy compaction property”, meaning that for many signals only the first few DCT coefficients have significant magnitude. Zeroing out the other coefficients leads to a small reconstruction error, a fact which is exploited in lossy signal compression (e.g. JPEG compression).
The example below shows a signal x and two reconstructions (\(x_{20}\) and \(x_{15}\)) from the signal’s DCT coefficients. The signal \(x_{20}\) is reconstructed from the first 20 DCT coefficients, \(x_{15}\) is reconstructed from the first 15 DCT coefficients. It can be seen that the relative error of using 20 coefficients is still very small (~0.1%), but provides a five-fold compression rate.
>>> from scipy.fft import dct, idct
>>> import matplotlib.pyplot as plt
>>> N = 100
>>> t = np.linspace(0,20,N, endpoint=False)
>>> x = np.exp(-t/3)*np.cos(2*t)
>>> y = dct(x, norm='ortho')
>>> window = np.zeros(N)
>>> window[:20] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.0009872817275276098
>>> plt.plot(t, x, '-bx')
>>> plt.plot(t, yr, 'ro')
>>> window = np.zeros(N)
>>> window[:15] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.06196643004256714
>>> plt.plot(t, yr, 'g+')
>>> plt.legend(['x', '$x_{20}$', '$x_{15}$'])
>>> plt.grid()
>>> plt.show()
Discrete Sine Transforms#
SciPy provides a DST [Mak] with the function dst and a corresponding IDST
with the function idst.
There are, theoretically, 8 types of the DST for different combinations of even/odd boundary conditions and boundary offsets [WPS], only the first 4 types are implemented in scipy.
Type I DST#
DST-I assumes the input is odd around n=-1 and n=N. SciPy uses the following
definition of the unnormalized DST-I (norm=None):
Note also that the DST-I is only supported for input size > 1. The
(unnormalized) DST-I is its own inverse, up to a factor of 2(N+1).
Type II DST#
DST-II assumes the input is odd around n=-1/2 and even around n=N. SciPy uses
the following definition of the unnormalized DST-II (norm=None):
Type III DST#
DST-III assumes the input is odd around n=-1 and even around n=N-1. SciPy uses
the following definition of the unnormalized DST-III (norm=None):
Type IV DST#
SciPy uses the following definition of the unnormalized DST-IV
(norm=None):
or, for norm='ortho':
DST and IDST#
The following example shows the relation between DST and IDST for different types and normalizations.
>>> from scipy.fft import dst, idst
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
The DST-II and DST-III are each other’s inverses, so for an orthonormal transform we return back to the original signal.
>>> dst(dst(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
Doing the same under default normalization, however, we pick up an extra scaling factor of \(2N=10\) since the forward transform is unnormalized.
>>> dst(dst(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
For this reason, we should use the function idst using the same type for both,
giving a correctly normalized result.
>>> idst(dst(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Analogous results can be seen for the DST-I, which is its own inverse up to a factor of \(2(N-1)\).
>>> dst(dst(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*(N+1) = 12
>>> dst(dst(x, type=1), type=1)
array([ 12., 24., 12., -12., 18.])
>>> # no scaling factor
>>> idst(dst(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
And for the DST-IV, which is also its own inverse up to a factor of \(2N\).
>>> dst(dst(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*N = 10
>>> dst(dst(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # no scaling factor
>>> idst(dst(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
Fast Hankel Transform#
SciPy provides the functions fht and ifht to perform the Fast
Hankel Transform (FHT) and its inverse (IFHT) on logarithmically-spaced input
arrays.
The FHT is the discretised version of the continuous Hankel transform defined by [Ham00]
with \(J_{\mu}\) the Bessel function of order \(\mu\). Under a change of variables \(r \to \log r\), \(k \to \log k\), this becomes
which is a convolution in logarithmic space. The FHT algorithm uses the FFT to perform this convolution on discrete input data.
Care must be taken to minimise numerical ringing due to the circular nature
of FFT convolution. To ensure that the low-ringing condition [Ham00] holds,
the output array can be slightly shifted by an offset computed using the
fhtoffset function.
References#
Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301.
Press, W., Teukolsky, S., Vetterline, W.T., and Flannery, B.P., 2007, Numerical Recipes: The Art of Scientific Computing, ch. 12-13. Cambridge Univ. Press, Cambridge, UK.
J. Makhoul, 1980, ‘A Fast Cosine Transform in One and Two Dimensions’, IEEE Transactions on acoustics, speech and signal processing vol. 28(1), pp. 27-34, DOI:10.1109/TASSP.1980.1163351
A. J. S. Hamilton, 2000, “Uncorrelated modes of the non-linear power spectrum”, MNRAS, 312, 257. DOI:10.1046/j.1365-8711.2000.03071.x