scipy.special.stdtrit#

scipy.special.stdtrit(df, p, out=None) = <ufunc 'stdtrit'>#

The p-th quantile of the student t distribution.

This function is the inverse of the student t distribution cumulative distribution function (CDF), returning t such that stdtr(df, t) = p.

Returns the argument t such that stdtr(df, t) is equal to p.

Parameters:

dfarray_like: Degrees of freedom
parray_like: Probability
outndarray, optional: Optional output array for the function results

Returns:

tscalar or ndarray: Value of t such that stdtr(df, t) == p

See also

stdtr: Student t CDF
stdtridf: inverse of stdtr with respect to df
scipy.stats.t: Student t distribution

Notes

The student t distribution is also available as scipy.stats.t. Calling stdtrit directly can improve performance compared to the ppf method of scipy.stats.t (see last example below).

Examples

stdtrit represents the inverse of the student t distribution CDF which is available as stdtr. Here, we calculate the CDF for df at x=1. stdtrit then returns 1 up to floating point errors given the same value for df and the computed CDF value.

>>> import numpy as np
>>> from scipy.special import stdtr, stdtrit
>>> import matplotlib.pyplot as plt
>>> df = 3
>>> x = 1
>>> cdf_value = stdtr(df, x)
>>> stdtrit(df, cdf_value)
0.9999999994418539

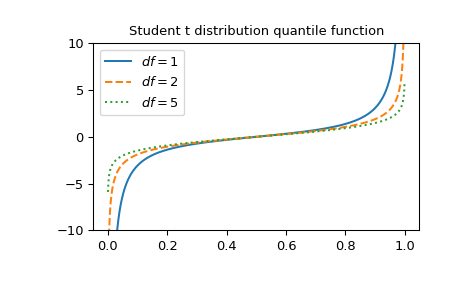
Plot the function for three different degrees of freedom.

>>> x = np.linspace(0, 1, 1000)
>>> parameters = [(1, "solid"), (2, "dashed"), (5, "dotted")]
>>> fig, ax = plt.subplots()
>>> for (df, linestyle) in parameters:
...     ax.plot(x, stdtrit(df, x), ls=linestyle, label=f"$df={df}$")
>>> ax.legend()
>>> ax.set_ylim(-10, 10)
>>> ax.set_title("Student t distribution quantile function")
>>> plt.show()

../../_images/scipy-special-stdtrit-1_00_00.png

The function can be computed for several degrees of freedom at the same time by providing a NumPy array or list for df:

>>> stdtrit([1, 2, 3], 0.7)
array([0.72654253, 0.6172134 , 0.58438973])

It is possible to calculate the function at several points for several different degrees of freedom simultaneously by providing arrays for df and p with shapes compatible for broadcasting. Compute stdtrit at 4 points for 3 degrees of freedom resulting in an array of shape 3x4.

>>> dfs = np.array([[1], [2], [3]])
>>> p = np.array([0.2, 0.4, 0.7, 0.8])
>>> dfs.shape, p.shape
((3, 1), (4,))

>>> stdtrit(dfs, p)
array([[-1.37638192, -0.3249197 ,  0.72654253,  1.37638192],
       [-1.06066017, -0.28867513,  0.6172134 ,  1.06066017],
       [-0.97847231, -0.27667066,  0.58438973,  0.97847231]])

The t distribution is also available as scipy.stats.t. Calling stdtrit directly can be much faster than calling the ppf method of scipy.stats.t. To get the same results, one must use the following parametrization: scipy.stats.t(df).ppf(x) = stdtrit(df, x).

>>> from scipy.stats import t
>>> df, x = 3, 0.5
>>> stdtrit_result = stdtrit(df, x)  # this can be faster than below
>>> stats_result = t(df).ppf(x)
>>> stats_result == stdtrit_result  # test that results are equal
True