scipy.special.stdtr#
- scipy.special.stdtr(df, t, out=None) = <ufunc 'stdtr'>#
Student t distribution cumulative distribution function
Returns the integral:
\[\frac{\Gamma((df+1)/2)}{\sqrt{\pi df} \Gamma(df/2)} \int_{-\infty}^t (1+x^2/df)^{-(df+1)/2}\, dx\]- Parameters:
- dfarray_like
Degrees of freedom
- tarray_like
Upper bound of the integral
- outndarray, optional
Optional output array for the function results
- Returns:
- scalar or ndarray
Value of the Student t CDF at t
See also
stdtridfinverse of stdtr with respect to df
stdtritinverse of stdtr with respect to t
scipy.stats.tstudent t distribution
Notes
The student t distribution is also available as
scipy.stats.t. Callingstdtrdirectly can improve performance compared to thecdfmethod ofscipy.stats.t(see last example below).The function is computed using the Boost Math library [1], which relies on the incomplete beta function.
Array API Standard Support
stdtrhas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
⛔
JAX
✅
✅
Dask
✅
n/a
See Support for the array API standard for more information.
References
[1]Boost C++ Libraries, http://www.boost.org/
Examples
Calculate the function for
df=3att=1.>>> import numpy as np >>> from scipy.special import stdtr >>> import matplotlib.pyplot as plt >>> stdtr(3, 1) 0.8044988905221148
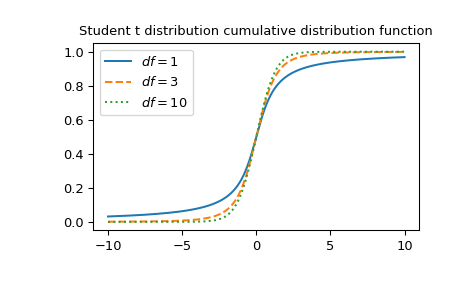
Plot the function for three different degrees of freedom.
>>> x = np.linspace(-10, 10, 1000) >>> fig, ax = plt.subplots() >>> parameters = [(1, "solid"), (3, "dashed"), (10, "dotted")] >>> for (df, linestyle) in parameters: ... ax.plot(x, stdtr(df, x), ls=linestyle, label=f"$df={df}$") >>> ax.legend() >>> ax.set_title("Student t distribution cumulative distribution function") >>> plt.show()
The function can be computed for several degrees of freedom at the same time by providing a NumPy array or list for df:
>>> stdtr([1, 2, 3], 1) array([0.75 , 0.78867513, 0.80449889])
It is possible to calculate the function at several points for several different degrees of freedom simultaneously by providing arrays for df and t with shapes compatible for broadcasting. Compute
stdtrat 4 points for 3 degrees of freedom resulting in an array of shape 3x4.>>> dfs = np.array([[1], [2], [3]]) >>> t = np.array([2, 4, 6, 8]) >>> dfs.shape, t.shape ((3, 1), (4,))
>>> stdtr(dfs, t) array([[0.85241638, 0.92202087, 0.94743154, 0.96041658], [0.90824829, 0.97140452, 0.98666426, 0.99236596], [0.93033702, 0.98599577, 0.99536364, 0.99796171]])
The t distribution is also available as
scipy.stats.t. Callingstdtrdirectly can be much faster than calling thecdfmethod ofscipy.stats.t. To get the same results, one must use the following parametrization:scipy.stats.t(df).cdf(x) = stdtr(df, x).>>> from scipy.stats import t >>> df, x = 3, 1 >>> stdtr_result = stdtr(df, x) # this can be faster than below >>> stats_result = t(df).cdf(x) >>> stats_result == stdtr_result # test that results are equal True