scipy.special.stdtrit#
- scipy.special.stdtrit(df, p, out=None) = <ufunc 'stdtrit'>#
The p-th quantile of the student t distribution.
This function is the inverse of the student t distribution cumulative distribution function (CDF), returning t such that stdtr(df, t) = p.
Returns the argument t such that stdtr(df, t) is equal to p.
- Parameters:
- dfarray_like
Degrees of freedom
- parray_like
Probability
- outndarray, optional
Optional output array for the function results
- Returns:
- tscalar or ndarray
Value of t such that
stdtr(df, t) == p
See also
stdtrStudent t CDF
stdtridfinverse of stdtr with respect to df
scipy.stats.tStudent t distribution
Notes
The student t distribution is also available as
scipy.stats.t. Callingstdtritdirectly can improve performance compared to theppfmethod ofscipy.stats.t(see last example below).Examples
stdtritrepresents the inverse of the student t distribution CDF which is available asstdtr. Here, we calculate the CDF fordfatx=1.stdtritthen returns1up to floating point errors given the same value for df and the computed CDF value.>>> import numpy as np >>> from scipy.special import stdtr, stdtrit >>> import matplotlib.pyplot as plt >>> df = 3 >>> x = 1 >>> cdf_value = stdtr(df, x) >>> stdtrit(df, cdf_value) 0.9999999994418539
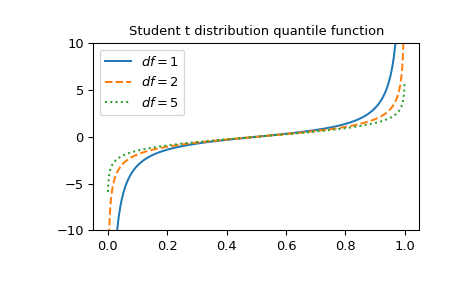
Plot the function for three different degrees of freedom.
>>> x = np.linspace(0, 1, 1000) >>> parameters = [(1, "solid"), (2, "dashed"), (5, "dotted")] >>> fig, ax = plt.subplots() >>> for (df, linestyle) in parameters: ... ax.plot(x, stdtrit(df, x), ls=linestyle, label=f"$df={df}$") >>> ax.legend() >>> ax.set_ylim(-10, 10) >>> ax.set_title("Student t distribution quantile function") >>> plt.show()
The function can be computed for several degrees of freedom at the same time by providing a NumPy array or list for df:
>>> stdtrit([1, 2, 3], 0.7) array([0.72654253, 0.6172134 , 0.58438973])
It is possible to calculate the function at several points for several different degrees of freedom simultaneously by providing arrays for df and p with shapes compatible for broadcasting. Compute
stdtritat 4 points for 3 degrees of freedom resulting in an array of shape 3x4.>>> dfs = np.array([[1], [2], [3]]) >>> p = np.array([0.2, 0.4, 0.7, 0.8]) >>> dfs.shape, p.shape ((3, 1), (4,))
>>> stdtrit(dfs, p) array([[-1.37638192, -0.3249197 , 0.72654253, 1.37638192], [-1.06066017, -0.28867513, 0.6172134 , 1.06066017], [-0.97847231, -0.27667066, 0.58438973, 0.97847231]])
The t distribution is also available as
scipy.stats.t. Callingstdtritdirectly can be much faster than calling theppfmethod ofscipy.stats.t. To get the same results, one must use the following parametrization:scipy.stats.t(df).ppf(x) = stdtrit(df, x).>>> from scipy.stats import t >>> df, x = 3, 0.5 >>> stdtrit_result = stdtrit(df, x) # this can be faster than below >>> stats_result = t(df).ppf(x) >>> stats_result == stdtrit_result # test that results are equal True