scipy.signal.

stft#

scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary='zeros', padded=True, axis=-1, scaling='spectrum')[source]#

Compute the Short Time Fourier Transform (legacy function).

STFTs can be used as a way of quantifying the change of a nonstationary signal’s frequency and phase content over time.

Legacy

This function is considered legacy and will no longer receive updates. This could also mean it will be removed in future SciPy versions. ShortTimeFFT is a newer STFT / ISTFT implementation with more features. A comparison between the implementations can be found in the Short-Time Fourier Transform section of the SciPy User Guide.

Parameters:

xarray_like: Time series of measurement values
fsfloat, optional: Sampling frequency of the x time series. Defaults to 1.0.
windowstr or tuple or array_like, optional: Desired window to use. If window is a string or tuple, it is passed to get_window to generate the window values, which are DFT-even by default. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a Hann window.
npersegint, optional: Length of each segment. Defaults to 256.
noverlapint, optional: Number of points to overlap between segments. If None, noverlap = nperseg // 2. Defaults to None. When specified, the COLA constraint must be met (see Notes below).
nfftint, optional: Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.
detrendstr or function or False, optional: Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to the detrend function. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to False.
return_onesidedbool, optional: If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Defaults to True, but for complex data, a two-sided spectrum is always returned.
boundarystr or None, optional: Specifies whether the input signal is extended at both ends, and how to generate the new values, in order to center the first windowed segment on the first input point. This has the benefit of enabling reconstruction of the first input point when the employed window function starts at zero. Valid options are ['even', 'odd', 'constant', 'zeros', None]. Defaults to ‘zeros’, for zero padding extension. I.e. [1, 2, 3, 4] is extended to [0, 1, 2, 3, 4, 0] for nperseg=3.
paddedbool, optional: Specifies whether the input signal is zero-padded at the end to make the signal fit exactly into an integer number of window segments, so that all of the signal is included in the output. Defaults to True. Padding occurs after boundary extension, if boundary is not None, and padded is True, as is the default.
axisint, optional: Axis along which the STFT is computed; the default is over the last axis (i.e. axis=-1).
scaling: {‘spectrum’, ‘psd’}: The default ‘spectrum’ scaling allows each frequency line of Zxx to be interpreted as a magnitude spectrum. The ‘psd’ option scales each line to a power spectral density - it allows to calculate the signal’s energy by numerically integrating over abs(Zxx)**2.

Added in version 1.9.0.

Returns:

fndarray: Array of sample frequencies.
tndarray: Array of segment times.
Zxxndarray: STFT of x. By default, the last axis of Zxx corresponds to the segment times.

See also

istft: Inverse Short Time Fourier Transform
ShortTimeFFT: Newer STFT/ISTFT implementation providing more features.
check_COLA: Check whether the Constant OverLap Add (COLA) constraint is met
check_NOLA: Check whether the Nonzero Overlap Add (NOLA) constraint is met
welch: Power spectral density by Welch’s method.
spectrogram: Spectrogram by Welch’s method.
csd: Cross spectral density by Welch’s method.
lombscargle: Lomb-Scargle periodogram for unevenly sampled data

Notes

In order to enable inversion of an STFT via the inverse STFT in istft, the signal windowing must obey the constraint of “Nonzero OverLap Add” (NOLA), and the input signal must have complete windowing coverage (i.e. (x.shape[axis] - nperseg) % (nperseg-noverlap) == 0). The padded argument may be used to accomplish this.

Given a time-domain signal \(x[n]\), a window \(w[n]\), and a hop size \(H\) = nperseg - noverlap, the windowed frame at time index \(t\) is given by

\[x_{t}[n]=x[n]w[n-tH]\]

The overlap-add (OLA) reconstruction equation is given by

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

The NOLA constraint ensures that every normalization term that appears in the denomimator of the OLA reconstruction equation is nonzero. Whether a choice of window, nperseg, and noverlap satisfy this constraint can be tested with check_NOLA.

Added in version 0.19.0.

References

[1]

Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time Signal Processing”, Prentice Hall, 1999.

[2]

Daniel W. Griffin, Jae S. Lim “Signal Estimation from Modified Short-Time Fourier Transform”, IEEE 1984, 10.1109/TASSP.1984.1164317

Examples

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

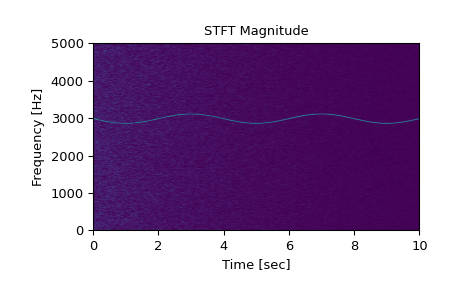
Generate a test signal, a 2 Vrms sine wave whose frequency is slowly modulated around 3kHz, corrupted by white noise of exponentially decreasing magnitude sampled at 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

Compute and plot the STFT’s magnitude.

>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000)
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

../../_images/scipy-signal-stft-1_00_00.png

Compare the energy of the signal x with the energy of its STFT:

>>> E_x = sum(x**2) / fs  # Energy of x
>>> # Calculate a two-sided STFT with PSD scaling:
>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000, return_onesided=False,
...                         scaling='psd')
>>> # Integrate numerically over abs(Zxx)**2:
>>> df, dt = f[1] - f[0], t[1] - t[0]
>>> E_Zxx = sum(np.sum(Zxx.real**2 + Zxx.imag**2, axis=0) * df) * dt
>>> # The energy is the same, but the numerical errors are quite large:
>>> np.isclose(E_x, E_Zxx, rtol=1e-2)
True