csd#
- scipy.signal.csd(x, y, fs=1.0, window='hann_periodic', nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, average='mean')[source]#
Estimate the cross power spectral density, Pxy, using Welch’s method.
- Parameters:
- xarray_like
Time series of measurement values
- yarray_like
Time series of measurement values
- fsfloat, optional
Sampling frequency of the x and y time series. Defaults to 1.0.
- windowstr or tuple or array_like, optional
Desired window to use. If window is a string or tuple, it is passed to
get_windowto generate the window values, which are DFT-even by default. Seeget_windowfor a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a periodic Hann window.- npersegint, optional
Length of each segment. Defaults to None, but if window is str or tuple, is set to 256, and if window is array_like, is set to the length of the window.
- noverlap: int, optional
Number of points to overlap between segments. If None,
noverlap = nperseg // 2. Defaults to None and may not be greater than nperseg.- nfftint, optional
Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.
- detrendstr or function or False, optional
Specifies how to detrend each segment. If
detrendis a string, it is passed as the type argument to thedetrendfunction. If it is a function, it takes a segment and returns a detrended segment. Ifdetrendis False, no detrending is done. Defaults to ‘constant’.- return_onesidedbool, optional
If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Defaults to True, but for complex data, a two-sided spectrum is always returned.
- scaling{ ‘density’, ‘spectrum’ }, optional
Selects between computing the cross spectral density (‘density’) where Pxy has units of V**2/Hz and computing the cross spectrum (‘spectrum’) where Pxy has units of V**2, if x and y are measured in V and fs is measured in Hz. Defaults to ‘density’
- axisint, optional
Axis along which the CSD is computed for both inputs; the default is over the last axis (i.e.
axis=-1).- average{ ‘mean’, ‘median’ }, optional
Method to use when averaging periodograms. If the spectrum is complex, the average is computed separately for the real and imaginary parts. Defaults to ‘mean’.
Added in version 1.2.0.
- Returns:
- fndarray
Array of sample frequencies.
- Pxyndarray
Cross spectral density or cross power spectrum of x,y.
See also
periodogramSimple, optionally modified periodogram
lombscargleLomb-Scargle periodogram for unevenly sampled data
welchPower spectral density by Welch’s method. [Equivalent to csd(x,x)]
coherenceMagnitude squared coherence by Welch’s method.
Notes
By convention, Pxy is computed with the conjugate FFT of X multiplied by the FFT of Y.
If the input series differ in length, the shorter series will be zero-padded to match.
An appropriate amount of overlap will depend on the choice of window and on your requirements. For the default Hann window an overlap of 50% is a reasonable trade-off between accurately estimating the signal power, while not over counting any of the data. Narrower windows may require a larger overlap.
The ratio of the cross spectrum (
scaling='spectrum') divided by the cross spectral density (scaling='density') is the constant factor ofsum(abs(window)**2)*fs / abs(sum(window))**2. If return_onesided isTrue, the values of the negative frequencies are added to values of the corresponding positive ones.Consult the Spectral Analysis section of the SciPy User Guide for a discussion of the scalings of a spectral density and an (amplitude) spectrum.
Welch’s method may be interpreted as taking the average over the time slices of a (cross-) spectrogram. Internally, this function utilizes the
ShortTimeFFTto determine the required (cross-) spectrogram. An example below illustrates that it is straightforward to calculate Pxy directly with theShortTimeFFT. However, there are some notable differences in the behavior of theShortTimeFFT:There is no direct
ShortTimeFFTequivalent for thecsdparameter combinationreturn_onesided=True, scaling='density', sincefft_mode='onesided2X'requires'psd'scaling. The is due tocsdreturning the doubled squared magnitude in this case, which does not have a sensible interpretation.ShortTimeFFTuses float64 / complex128 internally, which is due to the behavior of the utilizedfftmodule. Thus, those are the dtypes being returned. Thecsdfunction casts the return values to float32 / complex64 if the input is float32 / complex64 as well.The
csdfunction calculatesnp.conj(Sx[q,p]) * Sy[q,p], whereasspectrogramcalculatesSx[q,p] * np.conj(Sy[q,p])whereSx[q,p],Sy[q,p]are the STFTs of x and y. Also, the window positioning is different.
Added in version 0.16.0.
Array API Standard Support
csdhas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
⛔
⛔
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
References
[1]P. Welch, “The use of the fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms”, IEEE Trans. Audio Electroacoust. vol. 15, pp. 70-73, 1967.
[2]Rabiner, Lawrence R., and B. Gold. “Theory and Application of Digital Signal Processing” Prentice-Hall, pp. 414-419, 1975
Examples
The following example plots the cross power spectral density of two signals with some common features:
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() ... ... # Generate two test signals with some common features: >>> N, fs = 100_000, 10e3 # number of samples and sampling frequency >>> amp, freq = 20, 1234.0 # amplitude and frequency of utilized sine signal >>> noise_power = 0.001 * fs / 2 >>> time = np.arange(N) / fs >>> b, a = signal.butter(2, 0.25, 'low') >>> x = rng.normal(scale=np.sqrt(noise_power), size=time.shape) >>> y = signal.lfilter(b, a, x) >>> x += amp*np.sin(2*np.pi*freq*time) >>> y += rng.normal(scale=0.1*np.sqrt(noise_power), size=time.shape) ... ... # Compute and plot the magnitude of the cross spectral density: >>> nperseg, noverlap, win = 1024, 512, 'hann' >>> f, Pxy = signal.csd(x, y, fs, win, nperseg, noverlap) >>> fig0, ax0 = plt.subplots(tight_layout=True) >>> ax0.set_title(f"CSD ({win.title()}-window, {nperseg=}, {noverlap=})") >>> ax0.set(xlabel="Frequency $f$ in kHz", ylabel="CSD Magnitude in V²/Hz") >>> ax0.semilogy(f/1e3, np.abs(Pxy)) >>> ax0.grid() >>> plt.show()
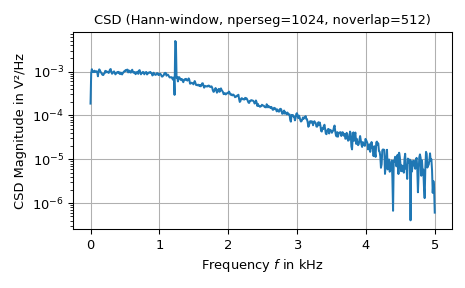
The cross spectral density is calculated by taking the average over the time slices of a spectrogram:
>>> SFT = signal.ShortTimeFFT.from_window('hann', fs, nperseg, noverlap, ... scale_to='psd', fft_mode='onesided2X', ... phase_shift=None) >>> Sxy1 = SFT.spectrogram(y, x, detr='constant', k_offset=nperseg//2, ... p0=0, p1=(N-noverlap) // SFT.hop) >>> Pxy1 = Sxy1.mean(axis=-1) >>> np.allclose(Pxy, Pxy1) # same result as with csd() True
As discussed in the Notes section, the results of using an approach analogous to the code snippet above and the
csdfunction may deviate due to implementation details.Note that the code snippet above can be easily adapted to determine other statistical properties than the mean value.