lombscargle#
- scipy.signal.lombscargle(x, y, freqs, *, precenter=<object object>, normalize=False, weights=None, floating_mean=False)[source]#
Compute the generalized Lomb-Scargle periodogram.
The Lomb-Scargle periodogram was developed by Lomb [1] and further extended by Scargle [2] to find, and test the significance of weak periodic signals with uneven temporal sampling. The algorithm used here is based on a weighted least-squares fit of the form
y(ω) = a*cos(ω*x) + b*sin(ω*x) + c, where the fit is calculated for each frequency independently. This algorithm was developed by Zechmeister and Kürster which improves the Lomb-Scargle periodogram by enabling the weighting of individual samples and calculating an unknown y offset (also called a “floating-mean” model) [3]. For more details, and practical considerations, see the excellent reference on the Lomb-Scargle periodogram [4].When normalize is False (or “power”) (default) the computed periodogram is unnormalized, it takes the value
(A**2) * N/4for a harmonic signal with amplitude A for sufficiently large N. Where N is the length of x or y.When normalize is True (or “normalize”) the computed periodogram is normalized by the residuals of the data around a constant reference model (at zero).
When normalize is “amplitude” the computed periodogram is the complex representation of the amplitude and phase.
Input arrays should be 1-D of a real floating data type, which are converted into float64 arrays before processing.
Deprecated since version 1.19.0: Use of argument(s)
{'floating_mean', 'precenter', 'normalize', 'weights'}by position is deprecated; beginning in SciPy 1.19.0, these will be keyword-only.- Parameters:
- xarray_like
Sample times.
- yarray_like
Measurement values. Values are assumed to have a baseline of
y = 0. If there is a possibility of a y offset, it is recommended to set floating_mean to True.- freqsarray_like
Angular frequencies (e.g., having unit rad/s=2π/s for x having unit s) for output periodogram. Frequencies are normally >= 0, as any peak at
-freqwill also exist at+freq.- precenterbool, optional
Pre-center measurement values by subtracting the mean, if True. This is a legacy parameter and unnecessary if floating_mean is True.
Deprecated since version 1.17.0: The precenter argument is deprecated and will be removed in SciPy 1.19.0. The functionality can be substituted by passing
y - y.mean()to y.- normalizebool | str, optional
Compute normalized or complex (amplitude + phase) periodogram. Valid options are:
False/"power",True/"normalize", or"amplitude".- weightsarray_like, optional
Weights for each sample. Weights must be nonnegative.
- floating_meanbool, optional
Determines a y offset for each frequency independently, if True. Else the y offset is assumed to be 0.
- Returns:
- pgramarray_like
Lomb-Scargle periodogram.
- Raises:
- ValueError
If any of the input arrays x, y, freqs, or weights are not 1D, or if any are zero length. Or, if the input arrays x, y, and weights do not have the same shape as each other.
- ValueError
If any weight is < 0, or the sum of the weights is <= 0.
- ValueError
If the normalize parameter is not one of the allowed options.
See also
periodogramPower spectral density using a periodogram
welchPower spectral density by Welch’s method
csdCross spectral density by Welch’s method
Notes
The algorithm used will not automatically account for any unknown y offset, unless floating_mean is
True. Therefore, for most use cases, if there is a possibility of a y offset, it is recommended to set floating_mean toTrue. Furthermore, floating_mean accounts for sample weights, and will also correct for any bias due to consistently missing observations at peaks and/or troughs.The legacy concept of “pre-centering” entails removing the mean from parameter y before processing, i.e., passing
y - y.mean()instead of setting the parameter floating_mean toTrue.When the normalize parameter is “amplitude”, for any frequency in freqs that is below
(2*pi)/(x.max() - x.min()), the predicted amplitude will tend towards infinity. The concept of a “Nyquist frequency” limit (see Nyquist-Shannon sampling theorem) is not generally applicable to unevenly sampled data. Therefore, with unevenly sampled data, valid frequencies in freqs can often be much higher than expected for those familiar with methods like FFT.Array API Standard Support
lombscarglehas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
⛔
⛔
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
References
[1]N.R. Lomb “Least-squares frequency analysis of unequally spaced data”, Astrophysics and Space Science, vol 39, pp. 447-462, 1976 DOI:10.1007/bf00648343
[2]J.D. Scargle “Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data”, The Astrophysical Journal, vol 263, pp. 835-853, 1982 DOI:10.1086/160554
[3]M. Zechmeister and M. Kürster, “The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms,” Astronomy and Astrophysics, vol. 496, pp. 577-584, 2009 DOI:10.1051/0004-6361:200811296
[4]J.T. VanderPlas, “Understanding the Lomb-Scargle Periodogram,” The Astrophysical Journal Supplement Series, vol. 236, no. 1, p. 16, May 2018 DOI:10.3847/1538-4365/aab766
Examples
>>> import numpy as np >>> rng = np.random.default_rng()
First define some input parameters for the signal:
>>> A = 2. # amplitude >>> c = 2. # offset >>> w0 = 1. # rad/sec >>> nin = 150 >>> nout = 1002
Randomly generate sample times:
>>> x = rng.uniform(0, 10*np.pi, nin)
Plot a sine wave for the selected times:
>>> y = A * np.cos(w0*x) + c
Define the array of frequencies for which to compute the periodogram:
>>> w = np.linspace(0.25, 10, nout)
Calculate Lomb-Scargle periodogram for each of the normalize options:
>>> from scipy.signal import lombscargle >>> pgram_power = lombscargle(x, y, w, normalize=False) >>> pgram_norm = lombscargle(x, y, w, normalize=True) >>> pgram_amp = lombscargle(x, y, w, normalize='amplitude') ... >>> pgram_power_f = lombscargle(x, y, w, normalize=False, floating_mean=True) >>> pgram_norm_f = lombscargle(x, y, w, normalize=True, floating_mean=True) >>> pgram_amp_f = lombscargle(x, y, w, normalize='amplitude', floating_mean=True)
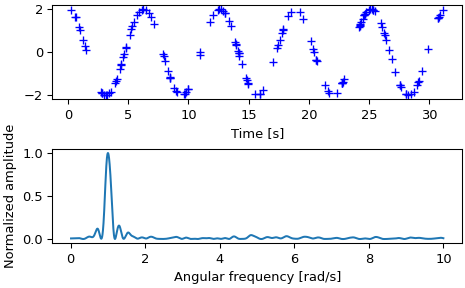
Now make a plot of the input data:
>>> import matplotlib.pyplot as plt >>> fig, (ax_t, ax_p, ax_n, ax_a) = plt.subplots(4, 1, figsize=(5, 6)) >>> ax_t.plot(x, y, 'b+') >>> ax_t.set_xlabel('Time [s]') >>> ax_t.set_ylabel('Amplitude')
Then plot the periodogram for each of the normalize options, as well as with and without floating_mean=True:
>>> ax_p.plot(w, pgram_power, label='default') >>> ax_p.plot(w, pgram_power_f, label='floating_mean=True') >>> ax_p.set_xlabel('Angular frequency [rad/s]') >>> ax_p.set_ylabel('Power') >>> ax_p.legend(prop={'size': 7}) ... >>> ax_n.plot(w, pgram_norm, label='default') >>> ax_n.plot(w, pgram_norm_f, label='floating_mean=True') >>> ax_n.set_xlabel('Angular frequency [rad/s]') >>> ax_n.set_ylabel('Normalized') >>> ax_n.legend(prop={'size': 7}) ... >>> ax_a.plot(w, np.abs(pgram_amp), label='default') >>> ax_a.plot(w, np.abs(pgram_amp_f), label='floating_mean=True') >>> ax_a.set_xlabel('Angular frequency [rad/s]') >>> ax_a.set_ylabel('Amplitude') >>> ax_a.legend(prop={'size': 7}) ... >>> plt.tight_layout() >>> plt.show()