scipy.special.fdtrc#
- scipy.special.fdtrc(dfn, dfd, x, out=None) = <ufunc 'fdtrc'>#
F survival function.
Returns the complemented F-distribution function (the integral of the density from x to infinity).
- Parameters:
- dfnarray_like
First parameter (positive float).
- dfdarray_like
Second parameter (positive float).
- xarray_like
Argument (nonnegative float).
- outndarray, optional
Optional output array for the function values
- Returns:
- yscalar or ndarray
The complemented F-distribution function with parameters dfn and dfd at x.
See also
fdtrF distribution cumulative distribution function
fdtriF distribution inverse cumulative distribution function
scipy.stats.fF distribution
Notes
The regularized incomplete beta function is used, according to the formula,
\[F(d_n, d_d; x) = I_{d_d/(d_d + xd_n)}(d_d/2, d_n/2).\]Wrapper for the Cephes [1] routine
fdtrc. The F distribution is also available asscipy.stats.f. Callingfdtrcdirectly can improve performance compared to thesfmethod ofscipy.stats.f(see last example below).References
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Examples
Calculate the function for
dfn=1anddfd=2atx=1.>>> import numpy as np >>> from scipy.special import fdtrc >>> fdtrc(1, 2, 1) 0.42264973081037427
Calculate the function at several points by providing a NumPy array for x.
>>> x = np.array([0.5, 2., 3.]) >>> fdtrc(1, 2, x) array([0.5527864 , 0.29289322, 0.22540333])
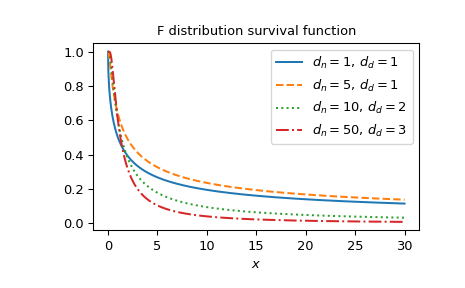
Plot the function for several parameter sets.
>>> import matplotlib.pyplot as plt >>> dfn_parameters = [1, 5, 10, 50] >>> dfd_parameters = [1, 1, 2, 3] >>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot'] >>> parameters_list = list(zip(dfn_parameters, dfd_parameters, ... linestyles)) >>> x = np.linspace(0, 30, 1000) >>> fig, ax = plt.subplots() >>> for parameter_set in parameters_list: ... dfn, dfd, style = parameter_set ... fdtrc_vals = fdtrc(dfn, dfd, x) ... ax.plot(x, fdtrc_vals, label=rf"$d_n={dfn},\, d_d={dfd}$", ... ls=style) >>> ax.legend() >>> ax.set_xlabel("$x$") >>> ax.set_title("F distribution survival function") >>> plt.show()
The F distribution is also available as
scipy.stats.f. Usingfdtrcdirectly can be much faster than calling thesfmethod ofscipy.stats.f, especially for small arrays or individual values. To get the same results one must use the following parametrization:stats.f(dfn, dfd).sf(x)=fdtrc(dfn, dfd, x).>>> from scipy.stats import f >>> dfn, dfd = 1, 2 >>> x = 1 >>> fdtrc_res = fdtrc(dfn, dfd, x) # this will often be faster than below >>> f_dist_res = f(dfn, dfd).sf(x) >>> f_dist_res == fdtrc_res # test that results are equal True