bootstrap#
- scipy.stats.bootstrap(data, statistic, *, n_resamples=9999, batch=None, vectorized=None, paired=False, axis=0, confidence_level=0.95, alternative='two-sided', method='BCa', bootstrap_result=None, rng=None, random_state=None)[source]#
Compute a two-sided bootstrap confidence interval of a statistic.
When method is
'percentile'and alternative is'two-sided', a bootstrap confidence interval is computed according to the following procedure.Resample the data: for each sample in data and for each of n_resamples, take a random sample of the original sample (with replacement) of the same size as the original sample.
Compute the bootstrap distribution of the statistic: for each set of resamples, compute the test statistic.
Determine the confidence interval: find the interval of the bootstrap distribution that is
symmetric about the median and
contains confidence_level of the resampled statistic values.
While the
'percentile'method is the most intuitive, it is rarely used in practice. Two more common methods are available,'basic'(‘reverse percentile’) and'BCa'(‘bias-corrected and accelerated’); they differ in how step 3 is performed.If the samples in data are taken at random from their respective distributions \(n\) times, the confidence interval returned by
bootstrapwill contain the true value of the statistic for those distributions approximately confidence_level\(\, \times \, n\) times.- Parameters:
- datasequence of array-like
Each element of data is a sample containing scalar observations from an underlying distribution. Elements of data must be broadcastable to the same shape (with the possible exception of the dimension specified by axis).
- statisticcallable
Statistic for which the confidence interval is to be calculated. statistic must be a callable that accepts
len(data)samples as separate arguments and returns the resulting statistic. If vectorized is setTrue, statistic must also accept a keyword argument axis and be vectorized to compute the statistic along the provided axis.- n_resamplesint, default:
9999 The number of resamples performed to form the bootstrap distribution of the statistic.
- batchint, optional
The number of resamples to process in each vectorized call to statistic. Memory usage is O( batch *
n), wherenis the sample size. Default isNone, in which casebatch = n_resamples(orbatch = max(n_resamples, n)formethod='BCa').- vectorizedbool, optional
If vectorized is set
False, statistic will not be passed keyword argument axis and is expected to calculate the statistic only for 1D samples. IfTrue, statistic will be passed keyword argument axis and is expected to calculate the statistic along axis when passed an ND sample array. IfNone(default), vectorized will be setTrueifaxisis a parameter of statistic. Use of a vectorized statistic typically reduces computation time.- pairedbool, default:
False Whether the statistic treats corresponding elements of the samples in data as paired. If True,
bootstrapresamples an array of indices and uses the same indices for all arrays in data; otherwise,bootstrapindependently resamples the elements of each array.- axisint, default:
0 The axis of the samples in data along which the statistic is calculated.
- confidence_levelfloat, default:
0.95 The confidence level of the confidence interval.
- alternative{‘two-sided’, ‘less’, ‘greater’}, default:
'two-sided' Choose
'two-sided'(default) for a two-sided confidence interval,'less'for a one-sided confidence interval with the lower bound at-np.inf, and'greater'for a one-sided confidence interval with the upper bound atnp.inf. The other bound of the one-sided confidence intervals is the same as that of a two-sided confidence interval with confidence_level twice as far from 1.0; e.g. the upper bound of a 95%'less'confidence interval is the same as the upper bound of a 90%'two-sided'confidence interval.- method{‘percentile’, ‘basic’, ‘bca’}, default:
'BCa' Whether to return the ‘percentile’ bootstrap confidence interval (
'percentile'), the ‘basic’ (AKA ‘reverse’) bootstrap confidence interval ('basic'), or the bias-corrected and accelerated bootstrap confidence interval ('BCa').- bootstrap_resultBootstrapResult, optional
Provide the result object returned by a previous call to
bootstrapto include the previous bootstrap distribution in the new bootstrap distribution. This can be used, for example, to change confidence_level, change method, or see the effect of performing additional resampling without repeating computations.- rng{None, int,
numpy.random.Generator}, optional If rng is passed by keyword, types other than
numpy.random.Generatorare passed tonumpy.random.default_rngto instantiate aGenerator. If rng is already aGeneratorinstance, then the provided instance is used. Specify rng for repeatable function behavior.If this argument is passed by position or random_state is passed by keyword, legacy behavior for the argument random_state applies:
If random_state is None (or
numpy.random), thenumpy.random.RandomStatesingleton is used.If random_state is an int, a new
RandomStateinstance is used, seeded with random_state.If random_state is already a
GeneratororRandomStateinstance then that instance is used.
Changed in version 1.15.0: As part of the SPEC-007 transition from use of
numpy.random.RandomStatetonumpy.random.Generator, this keyword was changed from random_state to rng. For an interim period, both keywords will continue to work, although only one may be specified at a time. After the interim period, function calls using the random_state keyword will emit warnings. The behavior of both random_state and rng are outlined above, but only the rng keyword should be used in new code.
- Returns:
- resBootstrapResult
An object with attributes:
- confidence_intervalConfidenceInterval
The bootstrap confidence interval as an instance of
collections.namedtuplewith attributes low and high.- bootstrap_distributionndarray
The bootstrap distribution, that is, the value of statistic for each resample. The last dimension corresponds with the resamples (e.g.
res.bootstrap_distribution.shape[-1] == n_resamples).- standard_errorfloat or ndarray
The bootstrap standard error, that is, the sample standard deviation of the bootstrap distribution.
- Warns:
DegenerateDataWarningGenerated when
method='BCa'and the bootstrap distribution is degenerate (e.g. all elements are identical).
Notes
Elements of the confidence interval may be NaN for
method='BCa'if the bootstrap distribution is degenerate (e.g. all elements are identical). In this case, consider using another method or inspecting data for indications that other analysis may be more appropriate (e.g. all observations are identical).Array API Standard Support
bootstraphas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
✅
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
References
[1]B. Efron and R. J. Tibshirani, An Introduction to the Bootstrap, Chapman & Hall/CRC, Boca Raton, FL, USA (1993)
[2]Nathaniel E. Helwig, “Bootstrap Confidence Intervals”, http://users.stat.umn.edu/~helwig/notes/bootci-Notes.pdf
[3]Bootstrapping (statistics), Wikipedia, https://en.wikipedia.org/wiki/Bootstrapping_%28statistics%29
Examples
Suppose we have sampled data from an unknown distribution.
>>> import numpy as np >>> rng = np.random.default_rng() >>> from scipy.stats import norm >>> dist = norm(loc=2, scale=4) # our "unknown" distribution >>> data = dist.rvs(size=100, random_state=rng)
We are interested in the standard deviation of the distribution.
>>> std_true = dist.std() # the true value of the statistic >>> print(std_true) 4.0 >>> std_sample = np.std(data) # the sample statistic >>> print(std_sample) 3.9460644295563863
The bootstrap is used to approximate the variability we would expect if we were to repeatedly sample from the unknown distribution and calculate the statistic of the sample each time. It does this by repeatedly resampling values from the original sample with replacement and calculating the statistic of each resample. This results in a “bootstrap distribution” of the statistic.
>>> import matplotlib.pyplot as plt >>> from scipy.stats import bootstrap >>> data = (data,) # samples must be in a sequence >>> res = bootstrap(data, np.std, confidence_level=0.9, rng=rng) >>> fig, ax = plt.subplots() >>> ax.hist(res.bootstrap_distribution, bins=25) >>> ax.set_title('Bootstrap Distribution') >>> ax.set_xlabel('statistic value') >>> ax.set_ylabel('frequency') >>> plt.show()
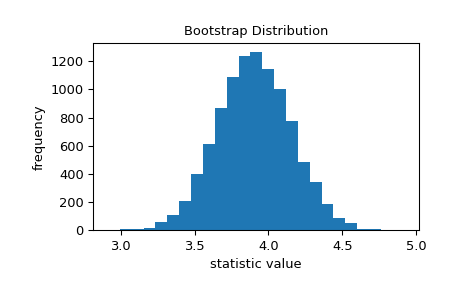
The standard error quantifies this variability. It is calculated as the standard deviation of the bootstrap distribution.
>>> res.standard_error 0.24427002125829136 >>> res.standard_error == np.std(res.bootstrap_distribution, ddof=1) True
The bootstrap distribution of the statistic is often approximately normal with scale equal to the standard error.
>>> x = np.linspace(3, 5) >>> pdf = norm.pdf(x, loc=std_sample, scale=res.standard_error) >>> fig, ax = plt.subplots() >>> ax.hist(res.bootstrap_distribution, bins=25, density=True) >>> ax.plot(x, pdf) >>> ax.set_title('Normal Approximation of the Bootstrap Distribution') >>> ax.set_xlabel('statistic value') >>> ax.set_ylabel('pdf') >>> plt.show()
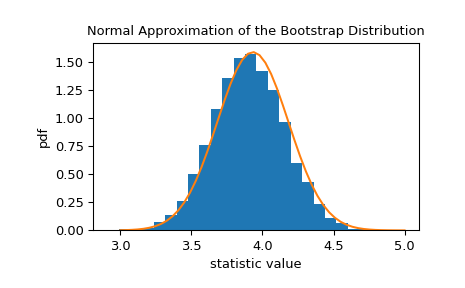
This suggests that we could construct a 90% confidence interval on the statistic based on quantiles of this normal distribution.
>>> norm.interval(0.9, loc=std_sample, scale=res.standard_error) (3.5442759991341726, 4.3478528599786)
Due to central limit theorem, this normal approximation is accurate for a variety of statistics and distributions underlying the samples; however, the approximation is not reliable in all cases. Because
bootstrapis designed to work with arbitrary underlying distributions and statistics, it uses more advanced techniques to generate an accurate confidence interval.>>> print(res.confidence_interval) ConfidenceInterval(low=3.57655333533867, high=4.382043696342881)
If we sample from the original distribution 100 times and form a bootstrap confidence interval for each sample, the confidence interval contains the true value of the statistic approximately 90% of the time.
>>> n_trials = 100 >>> ci_contains_true_std = 0 >>> for i in range(n_trials): ... data = (dist.rvs(size=100, random_state=rng),) ... res = bootstrap(data, np.std, confidence_level=0.9, ... n_resamples=999, rng=rng) ... ci = res.confidence_interval ... if ci[0] < std_true < ci[1]: ... ci_contains_true_std += 1 >>> print(ci_contains_true_std) 88
Rather than writing a loop, we can also determine the confidence intervals for all 100 samples at once.
>>> data = (dist.rvs(size=(n_trials, 100), random_state=rng),) >>> res = bootstrap(data, np.std, axis=-1, confidence_level=0.9, ... n_resamples=999, rng=rng) >>> ci_l, ci_u = res.confidence_interval
Here, ci_l and ci_u contain the confidence interval for each of the
n_trials = 100samples.>>> print(ci_l[:5]) [3.86401283 3.33304394 3.52474647 3.54160981 3.80569252] >>> print(ci_u[:5]) [4.80217409 4.18143252 4.39734707 4.37549713 4.72843584]
And again, approximately 90% contain the true value,
std_true = 4.>>> print(np.sum((ci_l < std_true) & (std_true < ci_u))) 93
bootstrapcan also be used to estimate confidence intervals of multi-sample statistics. For example, to get a confidence interval for the difference between means, we write a function that accepts two sample arguments and returns only the statistic. The use of theaxisargument ensures that all mean calculations are perform in a single vectorized call, which is faster than looping over pairs of resamples in Python.>>> def my_statistic(sample1, sample2, axis=-1): ... mean1 = np.mean(sample1, axis=axis) ... mean2 = np.mean(sample2, axis=axis) ... return mean1 - mean2
Here, we use the ‘percentile’ method with the default 95% confidence level.
>>> sample1 = norm.rvs(scale=1, size=100, random_state=rng) >>> sample2 = norm.rvs(scale=2, size=100, random_state=rng) >>> data = (sample1, sample2) >>> res = bootstrap(data, my_statistic, method='basic', rng=rng) >>> print(my_statistic(sample1, sample2)) 0.16661030792089523 >>> print(res.confidence_interval) ConfidenceInterval(low=-0.29087973240818693, high=0.6371338699912273)
The bootstrap estimate of the standard error is also available.
>>> print(res.standard_error) 0.238323948262459
Paired-sample statistics work, too. For example, consider the Pearson correlation coefficient.
>>> from scipy.stats import pearsonr >>> n = 100 >>> x = np.linspace(0, 10, n) >>> y = x + rng.uniform(size=n) >>> print(pearsonr(x, y)[0]) # element 0 is the statistic 0.9954306665125647
We wrap
pearsonrso that it returns only the statistic, ensuring that we use the axis argument because it is available.>>> def my_statistic(x, y, axis=-1): ... return pearsonr(x, y, axis=axis)[0]
We call
bootstrapusingpaired=True.>>> res = bootstrap((x, y), my_statistic, paired=True, rng=rng) >>> print(res.confidence_interval) ConfidenceInterval(low=0.9941504301315878, high=0.996377412215445)
The result object can be passed back into
bootstrapto perform additional resampling:>>> len(res.bootstrap_distribution) 9999 >>> res = bootstrap((x, y), my_statistic, paired=True, ... n_resamples=1000, rng=rng, ... bootstrap_result=res) >>> len(res.bootstrap_distribution) 10999
or to change the confidence interval options:
>>> res2 = bootstrap((x, y), my_statistic, paired=True, ... n_resamples=0, rng=rng, bootstrap_result=res, ... method='percentile', confidence_level=0.9) >>> np.testing.assert_equal(res2.bootstrap_distribution, ... res.bootstrap_distribution) >>> res.confidence_interval ConfidenceInterval(low=0.9941574828235082, high=0.9963781698210212)
without repeating computation of the original bootstrap distribution.