iirdesign#
- scipy.signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='ba', fs=None)[source]#
Complete IIR digital and analog filter design.
Given passband and stopband frequencies and gains, construct an analog or digital IIR filter of minimum order for a given basic type. Return the output in numerator, denominator (‘ba’), pole-zero (‘zpk’) or second order sections (‘sos’) form.
- Parameters:
- wp, wsfloat or array like, shape (2,)
Passband and stopband edge frequencies. Possible values are scalars (for lowpass and highpass filters) or ranges (for bandpass and bandstop filters). For digital filters, these are in the same units as fs. By default, fs is 2 half-cycles/sample, so these are normalized from 0 to 1, where 1 is the Nyquist frequency. For example:
Lowpass: wp = 0.2, ws = 0.3
Highpass: wp = 0.3, ws = 0.2
Bandpass: wp = [0.2, 0.5], ws = [0.1, 0.6]
Bandstop: wp = [0.1, 0.6], ws = [0.2, 0.5]
For analog filters, wp and ws are angular frequencies (e.g., rad/s). Note, that for bandpass and bandstop filters passband must lie strictly inside stopband or vice versa. Also note that the cutoff at the band edges for IIR filters is defined as half-power, so -3dB, not half-amplitude (-6dB) like for scipy.signal.fiwin.
- gpassfloat
The maximum loss in the passband (dB).
- gstopfloat
The minimum attenuation in the stopband (dB).
- analogbool, optional
When True, return an analog filter, otherwise a digital filter is returned.
- ftypestr, optional
The type of IIR filter to design:
Butterworth : ‘butter’
Chebyshev I : ‘cheby1’
Chebyshev II : ‘cheby2’
Cauer/elliptic: ‘ellip’
- output{‘ba’, ‘zpk’, ‘sos’}, optional
Filter form of the output:
second-order sections (recommended): ‘sos’
numerator/denominator (default) : ‘ba’
pole-zero : ‘zpk’
In general the second-order sections (‘sos’) form is recommended because inferring the coefficients for the numerator/denominator form (‘ba’) suffers from numerical instabilities. For reasons of backward compatibility the default form is the numerator/denominator form (‘ba’), where the ‘b’ and the ‘a’ in ‘ba’ refer to the commonly used names of the coefficients used.
Note: Using the second-order sections form (‘sos’) is sometimes associated with additional computational costs: for data-intense use cases it is therefore recommended to also investigate the numerator/denominator form (‘ba’).
- fsfloat, optional
The sampling frequency of the digital system.
Added in version 1.2.0.
- Returns:
- b, andarray, ndarray
Numerator (b) and denominator (a) polynomials of the IIR filter. Only returned if
output='ba'.- z, p, kndarray, ndarray, float
Zeros, poles, and system gain of the IIR filter transfer function. Only returned if
output='zpk'.- sosndarray
Second-order sections representation of the IIR filter. Only returned if
output='sos'.
See also
Notes
The
'sos'output parameter was added in 0.16.0.Array API Standard Support
iirdesignhas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
✅
JAX
✅
✅
Dask
✅
n/a
See Support for the array API standard for more information.
Examples
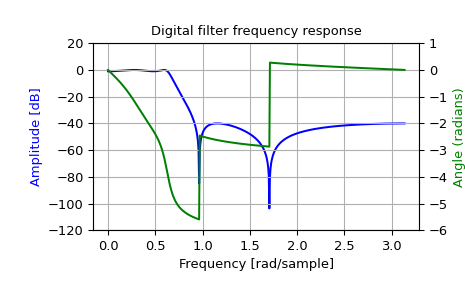
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import matplotlib.ticker
>>> wp = 0.2 >>> ws = 0.3 >>> gpass = 1 >>> gstop = 40
>>> system = signal.iirdesign(wp, ws, gpass, gstop) >>> w, h = signal.freqz(*system)
>>> fig, ax1 = plt.subplots() >>> ax1.set_title('Digital filter frequency response') >>> ax1.plot(w, 20 * np.log10(abs(h)), 'b') >>> ax1.set_ylabel('Amplitude [dB]', color='b') >>> ax1.set_xlabel('Frequency [rad/sample]') >>> ax1.grid(True) >>> ax1.set_ylim([-120, 20]) >>> ax2 = ax1.twinx() >>> phase = np.unwrap(np.angle(h)) >>> ax2.plot(w, phase, 'g') >>> ax2.set_ylabel('Phase [rad]', color='g') >>> ax2.grid(True) >>> ax2.axis('tight') >>> ax2.set_ylim([-6, 1]) >>> nticks = 8 >>> ax1.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks)) >>> ax2.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))