cheb1ord#
- scipy.signal.cheb1ord(wp, ws, gpass, gstop, analog=False, fs=None)[source]#
Chebyshev type I filter order selection.
Return the order of the lowest order digital or analog Chebyshev Type I filter that loses no more than gpass dB in the passband and has at least gstop dB attenuation in the stopband.
- Parameters:
- wp, wsfloat
Passband and stopband edge frequencies.
For digital filters, these are in the same units as fs. By default, fs is 2 half-cycles/sample, so these are normalized from 0 to 1, where 1 is the Nyquist frequency. (wp and ws are thus in half-cycles / sample.) For example:
Lowpass: wp = 0.2, ws = 0.3
Highpass: wp = 0.3, ws = 0.2
Bandpass: wp = [0.2, 0.5], ws = [0.1, 0.6]
Bandstop: wp = [0.1, 0.6], ws = [0.2, 0.5]
For analog filters, wp and ws are angular frequencies (e.g., rad/s).
- gpassfloat
The maximum loss in the passband (dB).
- gstopfloat
The minimum attenuation in the stopband (dB).
- analogbool, optional
When True, return an analog filter, otherwise a digital filter is returned.
- fsfloat, optional
The sampling frequency of the digital system.
Added in version 1.2.0.
- Returns:
See also
Examples
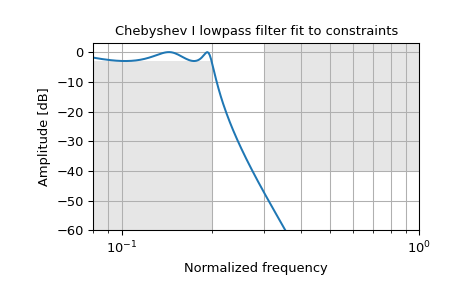
Design a digital lowpass filter such that the passband is within 3 dB up to 0.2*(fs/2), while rejecting at least -40 dB above 0.3*(fs/2). Plot its frequency response, showing the passband and stopband constraints in gray.
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np
>>> N, Wn = signal.cheb1ord(0.2, 0.3, 3, 40) >>> b, a = signal.cheby1(N, 3, Wn, 'low') >>> w, h = signal.freqz(b, a) >>> plt.semilogx(w / np.pi, 20 * np.log10(abs(h))) >>> plt.title('Chebyshev I lowpass filter fit to constraints') >>> plt.xlabel('Normalized frequency') >>> plt.ylabel('Amplitude [dB]') >>> plt.grid(which='both', axis='both') >>> plt.fill([.01, 0.2, 0.2, .01], [-3, -3, -99, -99], '0.9', lw=0) # stop >>> plt.fill([0.3, 0.3, 2, 2], [ 9, -40, -40, 9], '0.9', lw=0) # pass >>> plt.axis([0.08, 1, -60, 3]) >>> plt.show()