scipy.special.nbdtri#
- scipy.special.nbdtri(k, n, y, out=None) = <ufunc 'nbdtri'>#
Returns the inverse with respect to the parameter p of y = nbdtr(k, n, p), the negative binomial cumulative distribution function.
- Parameters:
- karray_like
The maximum number of allowed failures (nonnegative int).
- narray_like
The target number of successes (positive int).
- yarray_like
The probability of k or fewer failures before n successes (float).
- outndarray, optional
Optional output array for the function results
- Returns:
- pscalar or ndarray
Probability of success in a single event (float) such that nbdtr(k, n, p) = y.
See also
nbdtrCumulative distribution function of the negative binomial.
nbdtrcNegative binomial survival function.
scipy.stats.nbinomnegative binomial distribution.
nbdtrikInverse with respect to k of nbdtr(k, n, p).
nbdtrinInverse with respect to n of nbdtr(k, n, p).
scipy.stats.nbinomNegative binomial distribution
Notes
Wrapper for the Cephes [1] routine
nbdtri.The negative binomial distribution is also available as
scipy.stats.nbinom. Usingnbdtridirectly can improve performance compared to theppfmethod ofscipy.stats.nbinom.References
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Examples
nbdtriis the inverse ofnbdtrwith respect to p. Up to floating point errors the following holds:nbdtri(k, n, nbdtr(k, n, p))=p.>>> import numpy as np >>> from scipy.special import nbdtri, nbdtr >>> k, n, y = 5, 10, 0.2 >>> cdf_val = nbdtr(k, n, y) >>> nbdtri(k, n, cdf_val) 0.20000000000000004
Compute the function for
k=10andn=5at several points by providing a NumPy array or list for y.>>> y = np.array([0.1, 0.4, 0.8]) >>> nbdtri(3, 5, y) array([0.34462319, 0.51653095, 0.69677416])
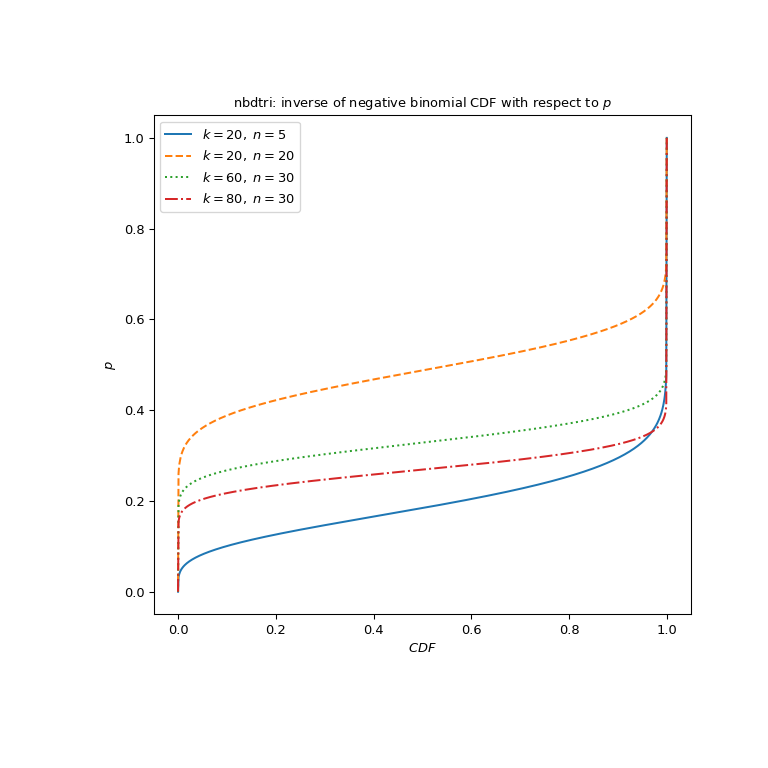
Plot the function for three different parameter sets.
>>> import matplotlib.pyplot as plt >>> n_parameters = [5, 20, 30, 30] >>> k_parameters = [20, 20, 60, 80] >>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot'] >>> parameters_list = list(zip(n_parameters, k_parameters, linestyles)) >>> cdf_vals = np.linspace(0, 1, 1000) >>> fig, ax = plt.subplots(figsize=(8, 8)) >>> for parameter_set in parameters_list: ... n, k, style = parameter_set ... nbdtri_vals = nbdtri(k, n, cdf_vals) ... ax.plot(cdf_vals, nbdtri_vals, label=rf"$k={k},\ n={n}$", ... ls=style) >>> ax.legend() >>> ax.set_ylabel("$p$") >>> ax.set_xlabel("$CDF$") >>> title = "nbdtri: inverse of negative binomial CDF with respect to $p$" >>> ax.set_title(title) >>> plt.show()
nbdtrican evaluate different parameter sets by providing arrays with shapes compatible for broadcasting for k, n and p. Here we compute the function for three different k at four locations p, resulting in a 3x4 array.>>> k = np.array([[5], [10], [15]]) >>> y = np.array([0.3, 0.5, 0.7, 0.9]) >>> k.shape, y.shape ((3, 1), (4,))
>>> nbdtri(k, 5, y) array([[0.37258157, 0.45169416, 0.53249956, 0.64578407], [0.24588501, 0.30451981, 0.36778453, 0.46397088], [0.18362101, 0.22966758, 0.28054743, 0.36066188]])