scipy.special.j0#
- scipy.special.j0(x, out=None) = <ufunc 'j0'>#
Bessel function of the first kind of order 0.
- Parameters:
- xarray_like
Argument (float).
- outndarray, optional
Optional output array for the function values
- Returns:
- Jscalar or ndarray
Value of the Bessel function of the first kind of order 0 at x.
See also
jvBessel function of real order and complex argument.
spherical_jnspherical Bessel functions.
Notes
The domain is divided into the intervals [0, 5] and (5, infinity). In the first interval the following rational approximation is used:
\[J_0(x) \approx (w - r_1^2)(w - r_2^2) \frac{P_3(w)}{Q_8(w)},\]where \(w = x^2\) and \(r_1\), \(r_2\) are the zeros of \(J_0\), and \(P_3\) and \(Q_8\) are polynomials of degrees 3 and 8, respectively.
In the second interval, the Hankel asymptotic expansion is employed with two rational functions of degree 6/6 and 7/7.
This function is a wrapper for the Cephes [1] routine
j0. It should not be confused with the spherical Bessel functions (seespherical_jn).References
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Examples
Calculate the function at one point:
>>> from scipy.special import j0 >>> j0(1.) 0.7651976865579665
Calculate the function at several points:
>>> import numpy as np >>> j0(np.array([-2., 0., 4.])) array([ 0.22389078, 1. , -0.39714981])
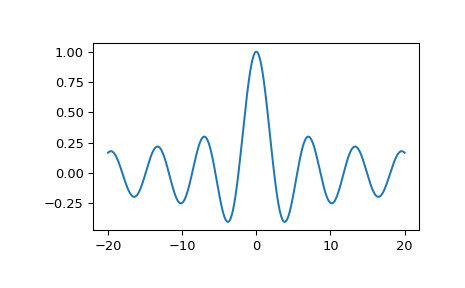
Plot the function from -20 to 20.
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> x = np.linspace(-20., 20., 1000) >>> y = j0(x) >>> ax.plot(x, y) >>> plt.show()