scipy.spatial.KDTree.
query_ball_tree#
- KDTree.query_ball_tree(other, r, p=2.0, eps=0.0)[source]#
Find all pairs of points between self and other whose distance is at most r.
- Parameters:
- otherKDTree instance
The tree containing points to search against.
- rfloat
The maximum distance, has to be positive.
- pfloat, optional
Which Minkowski norm to use. p has to meet the condition
1 <= p <= infinity.- epsfloat, optional
Approximate search. Branches of the tree are not explored if their nearest points are further than
r/(1+eps), and branches are added in bulk if their furthest points are nearer thanr * (1+eps). eps has to be non-negative.
- Returns:
- resultslist of lists
For each element
self.data[i]of this tree,results[i]is a list of the indices of its neighbors inother.data.
Examples
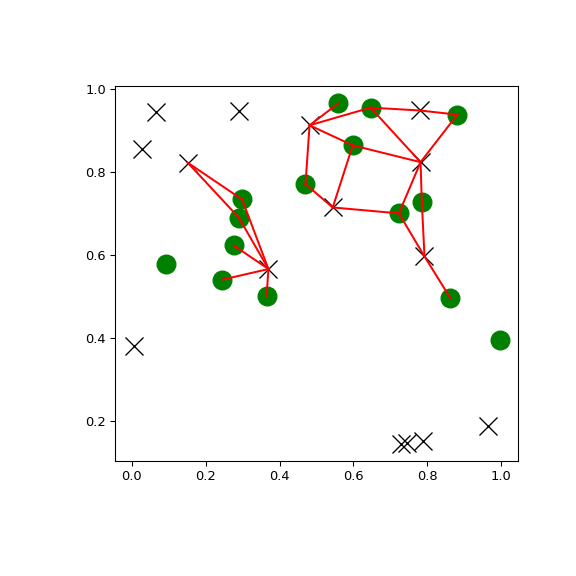
You can search all pairs of points between two kd-trees within a distance:
>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.spatial import KDTree >>> rng = np.random.default_rng() >>> points1 = rng.random((15, 2)) >>> points2 = rng.random((15, 2)) >>> plt.figure(figsize=(6, 6)) >>> plt.plot(points1[:, 0], points1[:, 1], "xk", markersize=14) >>> plt.plot(points2[:, 0], points2[:, 1], "og", markersize=14) >>> kd_tree1 = KDTree(points1) >>> kd_tree2 = KDTree(points2) >>> indexes = kd_tree1.query_ball_tree(kd_tree2, r=0.2) >>> for i in range(len(indexes)): ... for j in indexes[i]: ... plt.plot([points1[i, 0], points2[j, 0]], ... [points1[i, 1], points2[j, 1]], "-r") >>> plt.show()