zoom_fft#
- scipy.signal.zoom_fft(x, fn, m=None, *, fs=2, endpoint=False, axis=-1)[source]#
Compute the DFT of x only for frequencies in range fn.
- Parameters:
- xarray
The signal to transform.
- fnarray_like
A length-2 sequence [f1, f2] giving the frequency range, or a scalar, for which the range [0, fn] is assumed.
- mint, optional
The number of points to evaluate. The default is the length of x.
- fsfloat, optional
The sampling frequency. If
fs=10represented 10 kHz, for example, then f1 and f2 would also be given in kHz. The default sampling frequency is 2, so f1 and f2 should be in the range [0, 1] to keep the transform below the Nyquist frequency.- endpointbool, optional
If True, f2 is the last sample. Otherwise, it is not included. Default is False.
- axisint, optional
Axis over which to compute the FFT. If not given, the last axis is used.
- Returns:
- outndarray
The transformed signal. The Fourier transform will be calculated at the points f1, f1+df, f1+2df, …, f2, where df=(f2-f1)/m.
See also
ZoomFFTClass that creates a callable partial FFT function.
Notes
The defaults are chosen such that
signal.zoom_fft(x, 2)is equivalent tofft.fft(x)and, ifm > len(x), thatsignal.zoom_fft(x, 2, m)is equivalent tofft.fft(x, m).To graph the magnitude of the resulting transform, use:
plot(linspace(f1, f2, m, endpoint=False), abs(zoom_fft(x, [f1, f2], m)))
If the transform needs to be repeated, use
ZoomFFTto construct a specialized transform function which can be reused without recomputing constants.Array API Standard Support
zoom_ffthas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
⛔
⛔
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
Examples
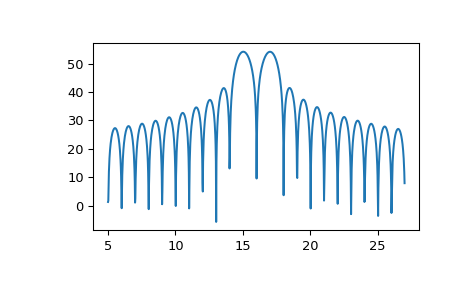
To plot the transform results use something like the following:
>>> import numpy as np >>> from scipy.signal import zoom_fft >>> t = np.linspace(0, 1, 1021) >>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t) >>> f1, f2 = 5, 27 >>> X = zoom_fft(x, [f1, f2], len(x), fs=1021) >>> f = np.linspace(f1, f2, len(x)) >>> import matplotlib.pyplot as plt >>> plt.plot(f, 20*np.log10(np.abs(X))) >>> plt.show()