scipy.signal.

resample_poly

scipy.signal.resample_poly(x, up, down, axis=0, window=('kaiser', 5.0), padtype='constant', cval=None)

Resample x along the given axis using polyphase filtering.

The signal x is upsampled by the factor up, a zero-phase low-pass FIR filter is applied, and then it is downsampled by the factor down. The resulting sample rate is up / down times the original sample rate. By default, values beyond the boundary of the signal are assumed to be zero during the filtering step.

Parameters:

xarray_like

The data to be resampled.

upint

The upsampling factor.

downint

The downsampling factor.

axisint, optional

The axis of x that is resampled. Default is 0.

windowstring, tuple, or array_like, optional

Desired window to use to design the low-pass filter, or the FIR filter coefficients to employ. See below for details.

padtypestring, optional

constant, line, mean, median, maximum, minimum or any of the other signal extension modes supported by scipy.signal.upfirdn. Changes assumptions on values beyond the boundary. If constant, assumed to be cval (default zero). If line assumed to continue a linear trend defined by the first and last points. mean, median, maximum and minimum work as in np.pad and assume that the values beyond the boundary are the mean, median, maximum or minimum respectively of the array along the axis.

Added in version 1.4.0.

cvalfloat, optional

Value to use if padtype=’constant’. Default is zero.

Added in version 1.4.0.

Returns:

resampled_xarray

The resampled array.

See also

decimate

Downsample the signal after applying an FIR or IIR filter.

resample

Resample up or down using the FFT method.

Notes

This polyphase method will likely be faster than the Fourier method in scipy.signal.resample when the number of samples is large and prime, or when the number of samples is large and up and down share a large greatest common denominator. The length of the FIR filter used will depend on max(up, down) // gcd(up, down), and the number of operations during polyphase filtering will depend on the filter length and down (see scipy.signal.upfirdn for details).

The argument window specifies the FIR low-pass filter design.

If window is an array_like it is assumed to be the FIR filter coefficients. Note that the FIR filter is applied after the upsampling step, so it should be designed to operate on a signal at a sampling frequency higher than the original by a factor of up//gcd(up, down). This function’s output will be centered with respect to this array, so it is best to pass a symmetric filter with an odd number of samples if, as is usually the case, a zero-phase filter is desired.

For any other type of window, the functions scipy.signal.get_window and scipy.signal.firwin are called to generate the appropriate filter coefficients.

The first sample of the returned vector is the same as the first sample of the input vector. The spacing between samples is changed from dx to dx * down / float(up).

Examples

Try it in your browser!

By default, the end of the resampled data rises to meet the first sample of the next cycle for the FFT method, and gets closer to zero for the polyphase method:

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(0, 10, 20, endpoint=False)
>>> y = np.cos(-x**2/6.0)
>>> f_fft = signal.resample(y, 100)
>>> f_poly = signal.resample_poly(y, 100, 20)
>>> xnew = np.linspace(0, 10, 100, endpoint=False)

>>> plt.plot(xnew, f_fft, 'b.-', xnew, f_poly, 'r.-')
>>> plt.plot(x, y, 'ko-')
>>> plt.plot(10, y[0], 'bo', 10, 0., 'ro')  # boundaries
>>> plt.legend(['resample', 'resamp_poly', 'data'], loc='best')
>>> plt.show()

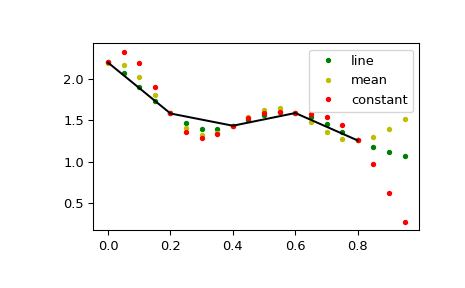
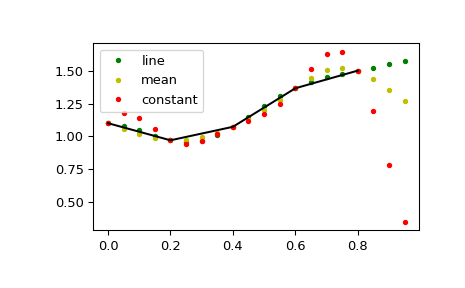
This default behaviour can be changed by using the padtype option:

>>> N = 5
>>> x = np.linspace(0, 1, N, endpoint=False)
>>> y = 2 + x**2 - 1.7*np.sin(x) + .2*np.cos(11*x)
>>> y2 = 1 + x**3 + 0.1*np.sin(x) + .1*np.cos(11*x)
>>> Y = np.stack([y, y2], axis=-1)
>>> up = 4
>>> xr = np.linspace(0, 1, N*up, endpoint=False)

>>> y2 = signal.resample_poly(Y, up, 1, padtype='constant')
>>> y3 = signal.resample_poly(Y, up, 1, padtype='mean')
>>> y4 = signal.resample_poly(Y, up, 1, padtype='line')

>>> for i in [0,1]:
...     plt.figure()
...     plt.plot(xr, y4[:,i], 'g.', label='line')
...     plt.plot(xr, y3[:,i], 'y.', label='mean')
...     plt.plot(xr, y2[:,i], 'r.', label='constant')
...     plt.plot(x, Y[:,i], 'k-')
...     plt.legend()
>>> plt.show()

Go BackOpen In Tab