fftn#
- scipy.fft.fftn(x, s=None, axes=None, norm=None, overwrite_x=False, workers=None, *, plan=None)[source]#
Compute the N-D discrete Fourier Transform.
This function computes the N-D discrete Fourier Transform over any number of axes in an M-D array by means of the Fast Fourier Transform (FFT).
- Parameters:
- xarray_like
Input array, can be complex.
- ssequence of ints, optional
Shape (length of each transformed axis) of the output (
s[0]refers to axis 0,s[1]to axis 1, etc.). This corresponds tonforfft(x, n). Along any axis, if the given shape is smaller than that of the input, the input is cropped. If it is larger, the input is padded with zeros. if s is not given, the shape of the input along the axes specified by axes is used.- axessequence of ints, optional
Axes over which to compute the FFT. If not given, the last
len(s)axes are used, or all axes if s is also not specified.- norm{“backward”, “ortho”, “forward”}, optional
Normalization mode (see
fft). Default is “backward”.- overwrite_xbool, optional
If True, the contents of x can be destroyed; the default is False. See
fftfor more details.- workersint, optional
Maximum number of workers to use for parallel computation. If negative, the value wraps around from
os.cpu_count(). Seefftfor more details.- planobject, optional
This argument is reserved for passing in a precomputed plan provided by downstream FFT vendors. It is currently not used in SciPy.
Added in version 1.5.0.
- Returns:
- outcomplex ndarray
The truncated or zero-padded input, transformed along the axes indicated by axes, or by a combination of s and x, as explained in the parameters section above.
- Raises:
- ValueError
If s and axes have different length.
- IndexError
If an element of axes is larger than the number of axes of x.
See also
Notes
The output, analogously to
fft, contains the term for zero frequency in the low-order corner of all axes, the positive frequency terms in the first half of all axes, the term for the Nyquist frequency in the middle of all axes and the negative frequency terms in the second half of all axes, in order of decreasingly negative frequency.Array API Standard Support
fftnhas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
✅
JAX
✅
✅
Dask
⚠️ computes graph
n/a
See Support for the array API standard for more information.
Examples
>>> import scipy.fft >>> import numpy as np >>> x = np.mgrid[:3, :3, :3][0] >>> scipy.fft.fftn(x, axes=(1, 2)) array([[[ 0.+0.j, 0.+0.j, 0.+0.j], # may vary [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]], [[ 9.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]], [[18.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]]]) >>> scipy.fft.fftn(x, (2, 2), axes=(0, 1)) array([[[ 2.+0.j, 2.+0.j, 2.+0.j], # may vary [ 0.+0.j, 0.+0.j, 0.+0.j]], [[-2.+0.j, -2.+0.j, -2.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]]])
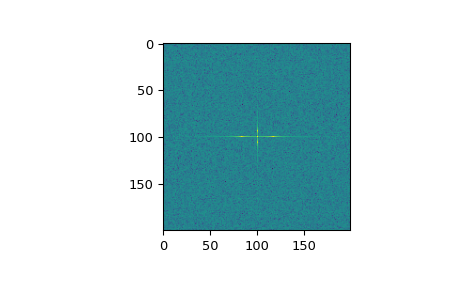
>>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> [X, Y] = np.meshgrid(2 * np.pi * np.arange(200) / 12, ... 2 * np.pi * np.arange(200) / 34) >>> S = np.sin(X) + np.cos(Y) + rng.uniform(0, 1, X.shape) >>> FS = scipy.fft.fftn(S) >>> plt.imshow(np.log(np.abs(scipy.fft.fftshift(FS))**2)) <matplotlib.image.AxesImage object at 0x...> >>> plt.show()