kmeans#
- scipy.cluster.vq.kmeans(obs, k_or_guess, iter=20, thresh=1e-05, check_finite=True, *, rng=None, seed=None)[source]#
Performs k-means on a set of observation vectors forming k clusters.
The k-means algorithm adjusts the classification of the observations into clusters and updates the cluster centroids until the position of the centroids is stable over successive iterations. In this implementation of the algorithm, the stability of the centroids is determined by comparing the absolute value of the change in the average Euclidean distance between the observations and their corresponding centroids against a threshold. This yields a code book mapping centroids to codes and vice versa.
- Parameters:
- obsndarray
Each row of the M by N array is an observation vector. The columns are the features seen during each observation. The features must be whitened first with the
whitenfunction.- k_or_guessint or ndarray
The number of centroids to generate. A code is assigned to each centroid, which is also the row index of the centroid in the code_book matrix generated.
The initial k centroids are chosen by randomly selecting observations from the observation matrix. Alternatively, passing a k by N array specifies the initial k centroids.
- iterint, optional
The number of times to run k-means, returning the codebook with the lowest distortion. This argument is ignored if initial centroids are specified with an array for the
k_or_guessparameter. This parameter does not represent the number of iterations of the k-means algorithm.- threshfloat, optional
Terminates the k-means algorithm if the change in distortion since the last k-means iteration is less than or equal to threshold.
- check_finitebool, optional
Whether to check that the input matrices contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs. Default: True
- rng{None, int,
numpy.random.Generator}, optional If rng is passed by keyword, types other than
numpy.random.Generatorare passed tonumpy.random.default_rngto instantiate aGenerator. If rng is already aGeneratorinstance, then the provided instance is used. Specify rng for repeatable function behavior.If this argument is passed by position or seed is passed by keyword, legacy behavior for the argument seed applies:
If seed is None (or
numpy.random), thenumpy.random.RandomStatesingleton is used.If seed is an int, a new
RandomStateinstance is used, seeded with seed.If seed is already a
GeneratororRandomStateinstance then that instance is used.
Changed in version 1.15.0: As part of the SPEC-007 transition from use of
numpy.random.RandomStatetonumpy.random.Generator, this keyword was changed from seed to rng. For an interim period, both keywords will continue to work, although only one may be specified at a time. After the interim period, function calls using the seed keyword will emit warnings. The behavior of both seed and rng are outlined above, but only the rng keyword should be used in new code.
- Returns:
- codebookndarray
A k by N array of k centroids. The ith centroid codebook[i] is represented with the code i. The centroids and codes generated represent the lowest distortion seen, not necessarily the globally minimal distortion. Note that the number of centroids is not necessarily the same as the
k_or_guessparameter, because centroids assigned to no observations are removed during iterations.- distortionfloat
The mean (non-squared) Euclidean distance between the observations passed and the centroids generated. Note the difference to the standard definition of distortion in the context of the k-means algorithm, which is the sum of the squared distances.
See also
Notes
For more functionalities or optimal performance, you can use sklearn.cluster.KMeans. This is a benchmark result of several implementations.
Array API Standard Support
kmeanshas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
✅
⛔
JAX
⚠️ no JIT
⛔
Dask
⚠️ computes graph
n/a
See Support for the array API standard for more information.
Examples
>>> import numpy as np >>> from scipy.cluster.vq import vq, kmeans, whiten >>> import matplotlib.pyplot as plt >>> features = np.array([[ 1.9,2.3], ... [ 1.5,2.5], ... [ 0.8,0.6], ... [ 0.4,1.8], ... [ 0.1,0.1], ... [ 0.2,1.8], ... [ 2.0,0.5], ... [ 0.3,1.5], ... [ 1.0,1.0]]) >>> whitened = whiten(features) >>> book = np.array((whitened[0],whitened[2])) >>> kmeans(whitened,book) (array([[ 2.3110306 , 2.86287398], # random [ 0.93218041, 1.24398691]]), 0.85684700941625547)
>>> codes = 3 >>> kmeans(whitened,codes) (array([[ 2.3110306 , 2.86287398], # random [ 1.32544402, 0.65607529], [ 0.40782893, 2.02786907]]), 0.5196582527686241)
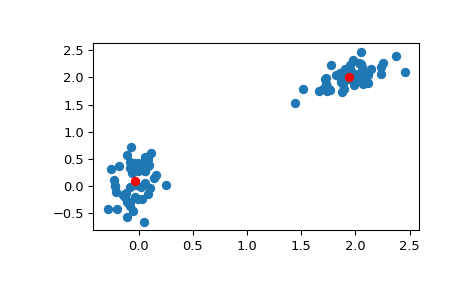
>>> # Create 50 datapoints in two clusters a and b >>> pts = 50 >>> rng = np.random.default_rng() >>> a = rng.multivariate_normal([0, 0], [[4, 1], [1, 4]], size=pts) >>> b = rng.multivariate_normal([30, 10], ... [[10, 2], [2, 1]], ... size=pts) >>> features = np.concatenate((a, b)) >>> # Whiten data >>> whitened = whiten(features) >>> # Find 2 clusters in the data >>> codebook, distortion = kmeans(whitened, 2) >>> # Plot whitened data and cluster centers in red >>> plt.scatter(whitened[:, 0], whitened[:, 1]) >>> plt.scatter(codebook[:, 0], codebook[:, 1], c='r') >>> plt.show()