Multidimensional image processing (scipy.ndimage)¶
Introduction¶
Image processing and analysis are generally seen as operations on
2-D arrays of values. There are, however, a number of
fields where images of higher dimensionality must be analyzed. Good
examples of these are medical imaging and biological imaging.
numpy is suited very well for this type of applications due to
its inherent multidimensional nature. The scipy.ndimage
packages provides a number of general image processing and analysis
functions that are designed to operate with arrays of arbitrary
dimensionality. The packages currently includes: functions for
linear and non-linear filtering, binary morphology, B-spline
interpolation, and object measurements.
Filter functions¶
The functions described in this section all perform some type of spatial filtering of the input array: the elements in the output are some function of the values in the neighborhood of the corresponding input element. We refer to this neighborhood of elements as the filter kernel, which is often rectangular in shape but may also have an arbitrary footprint. Many of the functions described below allow you to define the footprint of the kernel by passing a mask through the footprint parameter. For example, a cross-shaped kernel can be defined as follows:
>>> footprint = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> footprint
array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]])
Usually, the origin of the kernel is at the center calculated by dividing the dimensions of the kernel shape by two. For instance, the origin of a 1-D kernel of length three is at the second element. Take, for example, the correlation of a 1-D array with a filter of length 3 consisting of ones:
>>> from scipy.ndimage import correlate1d
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1])
array([0, 0, 1, 1, 1, 0, 0])
Sometimes, it is convenient to choose a different origin for the kernel. For this reason, most functions support the origin parameter, which gives the origin of the filter relative to its center. For example:
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1], origin = -1)
array([0, 1, 1, 1, 0, 0, 0])
The effect is a shift of the result towards the left. This feature will not be needed very often, but it may be useful, especially for filters that have an even size. A good example is the calculation of backward and forward differences:
>>> a = [0, 0, 1, 1, 1, 0, 0]
>>> correlate1d(a, [-1, 1]) # backward difference
array([ 0, 0, 1, 0, 0, -1, 0])
>>> correlate1d(a, [-1, 1], origin = -1) # forward difference
array([ 0, 1, 0, 0, -1, 0, 0])
We could also have calculated the forward difference as follows:
>>> correlate1d(a, [0, -1, 1])
array([ 0, 1, 0, 0, -1, 0, 0])
However, using the origin parameter instead of a larger kernel is more efficient. For multidimensional kernels, origin can be a number, in which case the origin is assumed to be equal along all axes, or a sequence giving the origin along each axis.
Since the output elements are a function of elements in the neighborhood of the input elements, the borders of the array need to be dealt with appropriately by providing the values outside the borders. This is done by assuming that the arrays are extended beyond their boundaries according to certain boundary conditions. In the functions described below, the boundary conditions can be selected using the mode parameter, which must be a string with the name of the boundary condition. The following boundary conditions are currently supported:
mode
description
example
“nearest”
use the value at the boundary
[1 2 3]->[1 1 2 3 3]
“wrap”
periodically replicate the array
[1 2 3]->[3 1 2 3 1]
“reflect”
reflect the array at the boundary
[1 2 3]->[1 1 2 3 3]
“mirror”
mirror the array at the boundary
[1 2 3]->[2 1 2 3 2]
“constant”
use a constant value, default is 0.0
[1 2 3]->[0 1 2 3 0]
The following synonyms are also supported for consistency with the interpolation routines:
mode
description
“grid-constant”
equivalent to “constant”*
“grid-mirror”
equivalent to “reflect”
“grid-wrap”
equivalent to “wrap”
* “grid-constant” and “constant” are equivalent for filtering operations, but have different behavior in interpolation functions. For API consistency, the filtering functions accept either name.
The “constant” mode is special since it needs an additional parameter to specify the constant value that should be used.
Note that modes mirror and reflect differ only in whether the sample at the boundary is repeated upon reflection. For mode mirror, the point of symmetry is exactly at the final sample, so that value is not repeated. This mode is also known as whole-sample symmetric since the point of symmetry falls on the final sample. Similarly, reflect is often refered to as half-sample symmetric as the point of symmetry is half a sample beyond the array boundary.
Note
The easiest way to implement such boundary conditions would be to copy the data to a larger array and extend the data at the borders according to the boundary conditions. For large arrays and large filter kernels, this would be very memory consuming, and the functions described below, therefore, use a different approach that does not require allocating large temporary buffers.
Correlation and convolution¶
The
correlate1dfunction calculates a 1-D correlation along the given axis. The lines of the array along the given axis are correlated with the given weights. The weights parameter must be a 1-D sequence of numbers.The function
correlateimplements multidimensional correlation of the input array with a given kernel.The
convolve1dfunction calculates a 1-D convolution along the given axis. The lines of the array along the given axis are convoluted with the given weights. The weights parameter must be a 1-D sequence of numbers.The function
convolveimplements multidimensional convolution of the input array with a given kernel.Note
A convolution is essentially a correlation after mirroring the kernel. As a result, the origin parameter behaves differently than in the case of a correlation: the results is shifted in the opposite direction.
Smoothing filters¶
The
gaussian_filter1dfunction implements a 1-D Gaussian filter. The standard deviation of the Gaussian filter is passed through the parameter sigma. Setting order = 0 corresponds to convolution with a Gaussian kernel. An order of 1, 2, or 3 corresponds to convolution with the first, second, or third derivatives of a Gaussian. Higher-order derivatives are not implemented.The
gaussian_filterfunction implements a multidimensional Gaussian filter. The standard deviations of the Gaussian filter along each axis are passed through the parameter sigma as a sequence or numbers. If sigma is not a sequence but a single number, the standard deviation of the filter is equal along all directions. The order of the filter can be specified separately for each axis. An order of 0 corresponds to convolution with a Gaussian kernel. An order of 1, 2, or 3 corresponds to convolution with the first, second, or third derivatives of a Gaussian. Higher-order derivatives are not implemented. The order parameter must be a number, to specify the same order for all axes, or a sequence of numbers to specify a different order for each axis.Note
The multidimensional filter is implemented as a sequence of 1-D Gaussian filters. The intermediate arrays are stored in the same data type as the output. Therefore, for output types with a lower precision, the results may be imprecise because intermediate results may be stored with insufficient precision. This can be prevented by specifying a more precise output type.
The
uniform_filter1dfunction calculates a 1-D uniform filter of the given size along the given axis.The
uniform_filterimplements a multidimensional uniform filter. The sizes of the uniform filter are given for each axis as a sequence of integers by the size parameter. If size is not a sequence, but a single number, the sizes along all axes are assumed to be equal.Note
The multidimensional filter is implemented as a sequence of 1-D uniform filters. The intermediate arrays are stored in the same data type as the output. Therefore, for output types with a lower precision, the results may be imprecise because intermediate results may be stored with insufficient precision. This can be prevented by specifying a more precise output type.
Filters based on order statistics¶
The
minimum_filter1dfunction calculates a 1-D minimum filter of the given size along the given axis.The
maximum_filter1dfunction calculates a 1-D maximum filter of the given size along the given axis.The
minimum_filterfunction calculates a multidimensional minimum filter. Either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint, if provided, must be an array that defines the shape of the kernel by its non-zero elements.The
maximum_filterfunction calculates a multidimensional maximum filter. Either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint, if provided, must be an array that defines the shape of the kernel by its non-zero elements.The
rank_filterfunction calculates a multidimensional rank filter. The rank may be less then zero, i.e., rank = -1 indicates the largest element. Either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint, if provided, must be an array that defines the shape of the kernel by its non-zero elements.The
percentile_filterfunction calculates a multidimensional percentile filter. The percentile may be less then zero, i.e., percentile = -20 equals percentile = 80. Either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint, if provided, must be an array that defines the shape of the kernel by its non-zero elements.The
median_filterfunction calculates a multidimensional median filter. Either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint if provided, must be an array that defines the shape of the kernel by its non-zero elements.
Derivatives¶
Derivative filters can be constructed in several ways. The function
gaussian_filter1d, described in
Smoothing filters, can be used to calculate
derivatives along a given axis using the order parameter. Other
derivative filters are the Prewitt and Sobel filters:
The
prewittfunction calculates a derivative along the given axis.The
sobelfunction calculates a derivative along the given axis.
The Laplace filter is calculated by the sum of the second derivatives along all axes. Thus, different Laplace filters can be constructed using different second-derivative functions. Therefore, we provide a general function that takes a function argument to calculate the second derivative along a given direction.
The function
generic_laplacecalculates a Laplace filter using the function passed throughderivative2to calculate second derivatives. The functionderivative2should have the following signaturederivative2(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)
It should calculate the second derivative along the dimension axis. If output is not
None, it should use that for the output and returnNone, otherwise it should return the result. mode, cval have the usual meaning.The extra_arguments and extra_keywords arguments can be used to pass a tuple of extra arguments and a dictionary of named arguments that are passed to
derivative2at each call.For example
>>> def d2(input, axis, output, mode, cval): ... return correlate1d(input, [1, -2, 1], axis, output, mode, cval, 0) ... >>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> from scipy.ndimage import generic_laplace >>> generic_laplace(a, d2) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
To demonstrate the use of the extra_arguments argument, we could do
>>> def d2(input, axis, output, mode, cval, weights): ... return correlate1d(input, weights, axis, output, mode, cval, 0,) ... >>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> generic_laplace(a, d2, extra_arguments = ([1, -2, 1],)) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
or
>>> generic_laplace(a, d2, extra_keywords = {'weights': [1, -2, 1]}) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
The following two functions are implemented using
generic_laplace by providing appropriate functions for the
second-derivative function:
The function
laplacecalculates the Laplace using discrete differentiation for the second derivative (i.e., convolution with[1, -2, 1]).The function
gaussian_laplacecalculates the Laplace filter usinggaussian_filterto calculate the second derivatives. The standard deviations of the Gaussian filter along each axis are passed through the parameter sigma as a sequence or numbers. If sigma is not a sequence but a single number, the standard deviation of the filter is equal along all directions.
The gradient magnitude is defined as the square root of the sum of the
squares of the gradients in all directions. Similar to the generic
Laplace function, there is a generic_gradient_magnitude
function that calculates the gradient magnitude of an array.
The function
generic_gradient_magnitudecalculates a gradient magnitude using the function passed throughderivativeto calculate first derivatives. The functionderivativeshould have the following signaturederivative(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)
It should calculate the derivative along the dimension axis. If output is not
None, it should use that for the output and returnNone, otherwise it should return the result. mode, cval have the usual meaning.The extra_arguments and extra_keywords arguments can be used to pass a tuple of extra arguments and a dictionary of named arguments that are passed to derivative at each call.
For example, the
sobelfunction fits the required signature>>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> from scipy.ndimage import sobel, generic_gradient_magnitude >>> generic_gradient_magnitude(a, sobel) array([[ 0. , 0. , 0. , 0. , 0. ], [ 0. , 1.41421356, 2. , 1.41421356, 0. ], [ 0. , 2. , 0. , 2. , 0. ], [ 0. , 1.41421356, 2. , 1.41421356, 0. ], [ 0. , 0. , 0. , 0. , 0. ]])
See the documentation of
generic_laplacefor examples of using the extra_arguments and extra_keywords arguments.
The sobel and prewitt functions fit the required
signature and can, therefore, be used directly with
generic_gradient_magnitude.
The function
gaussian_gradient_magnitudecalculates the gradient magnitude usinggaussian_filterto calculate the first derivatives. The standard deviations of the Gaussian filter along each axis are passed through the parameter sigma as a sequence or numbers. If sigma is not a sequence but a single number, the standard deviation of the filter is equal along all directions.
Generic filter functions¶
To implement filter functions, generic functions can be used that
accept a callable object that implements the filtering operation. The
iteration over the input and output arrays is handled by these generic
functions, along with such details as the implementation of the
boundary conditions. Only a callable object implementing a callback
function that does the actual filtering work must be provided. The
callback function can also be written in C and passed using a
PyCapsule (see Extending scipy.ndimage in C for more
information).
The
generic_filter1dfunction implements a generic 1-D filter function, where the actual filtering operation must be supplied as a python function (or other callable object). Thegeneric_filter1dfunction iterates over the lines of an array and callsfunctionat each line. The arguments that are passed tofunctionare 1-D arrays of thenumpy.float64type. The first contains the values of the current line. It is extended at the beginning and the end, according to the filter_size and origin arguments. The second array should be modified in-place to provide the output values of the line. For example, consider a correlation along one dimension:>>> a = np.arange(12).reshape(3,4) >>> correlate1d(a, [1, 2, 3]) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
The same operation can be implemented using
generic_filter1d, as follows:>>> def fnc(iline, oline): ... oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:] ... >>> from scipy.ndimage import generic_filter1d >>> generic_filter1d(a, fnc, 3) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
Here, the origin of the kernel was (by default) assumed to be in the middle of the filter of length 3. Therefore, each input line had been extended by one value at the beginning and at the end, before the function was called.
Optionally, extra arguments can be defined and passed to the filter function. The extra_arguments and extra_keywords arguments can be used to pass a tuple of extra arguments and/or a dictionary of named arguments that are passed to derivative at each call. For example, we can pass the parameters of our filter as an argument
>>> def fnc(iline, oline, a, b): ... oline[...] = iline[:-2] + a * iline[1:-1] + b * iline[2:] ... >>> generic_filter1d(a, fnc, 3, extra_arguments = (2, 3)) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
or
>>> generic_filter1d(a, fnc, 3, extra_keywords = {'a':2, 'b':3}) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
The
generic_filterfunction implements a generic filter function, where the actual filtering operation must be supplied as a python function (or other callable object). Thegeneric_filterfunction iterates over the array and callsfunctionat each element. The argument offunctionis a 1-D array of thenumpy.float64type that contains the values around the current element that are within the footprint of the filter. The function should return a single value that can be converted to a double precision number. For example, consider a correlation:>>> a = np.arange(12).reshape(3,4) >>> correlate(a, [[1, 0], [0, 3]]) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
The same operation can be implemented using generic_filter, as follows:
>>> def fnc(buffer): ... return (buffer * np.array([1, 3])).sum() ... >>> from scipy.ndimage import generic_filter >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]]) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
Here, a kernel footprint was specified that contains only two elements. Therefore, the filter function receives a buffer of length equal to two, which was multiplied with the proper weights and the result summed.
When calling
generic_filter, either the sizes of a rectangular kernel or the footprint of the kernel must be provided. The size parameter, if provided, must be a sequence of sizes or a single number, in which case the size of the filter is assumed to be equal along each axis. The footprint, if provided, must be an array that defines the shape of the kernel by its non-zero elements.Optionally, extra arguments can be defined and passed to the filter function. The extra_arguments and extra_keywords arguments can be used to pass a tuple of extra arguments and/or a dictionary of named arguments that are passed to derivative at each call. For example, we can pass the parameters of our filter as an argument
>>> def fnc(buffer, weights): ... weights = np.asarray(weights) ... return (buffer * weights).sum() ... >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_arguments = ([1, 3],)) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
or
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_keywords= {'weights': [1, 3]}) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
These functions iterate over the lines or elements starting at the
last axis, i.e., the last index changes the fastest. This order of
iteration is guaranteed for the case that it is important to adapt the
filter depending on spatial location. Here is an example of using a
class that implements the filter and keeps track of the current
coordinates while iterating. It performs the same filter operation as
described above for generic_filter, but additionally prints
the current coordinates:
>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc_class:
... def __init__(self, shape):
... # store the shape:
... self.shape = shape
... # initialize the coordinates:
... self.coordinates = [0] * len(shape)
...
... def filter(self, buffer):
... result = (buffer * np.array([1, 3])).sum()
... print(self.coordinates)
... # calculate the next coordinates:
... axes = list(range(len(self.shape)))
... axes.reverse()
... for jj in axes:
... if self.coordinates[jj] < self.shape[jj] - 1:
... self.coordinates[jj] += 1
... break
... else:
... self.coordinates[jj] = 0
... return result
...
>>> fnc = fnc_class(shape = (3,4))
>>> generic_filter(a, fnc.filter, footprint = [[1, 0], [0, 1]])
[0, 0]
[0, 1]
[0, 2]
[0, 3]
[1, 0]
[1, 1]
[1, 2]
[1, 3]
[2, 0]
[2, 1]
[2, 2]
[2, 3]
array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])
For the generic_filter1d function, the same approach works,
except that this function does not iterate over the axis that is being
filtered. The example for generic_filter1d then becomes this:
>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc1d_class:
... def __init__(self, shape, axis = -1):
... # store the filter axis:
... self.axis = axis
... # store the shape:
... self.shape = shape
... # initialize the coordinates:
... self.coordinates = [0] * len(shape)
...
... def filter(self, iline, oline):
... oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
... print(self.coordinates)
... # calculate the next coordinates:
... axes = list(range(len(self.shape)))
... # skip the filter axis:
... del axes[self.axis]
... axes.reverse()
... for jj in axes:
... if self.coordinates[jj] < self.shape[jj] - 1:
... self.coordinates[jj] += 1
... break
... else:
... self.coordinates[jj] = 0
...
>>> fnc = fnc1d_class(shape = (3,4))
>>> generic_filter1d(a, fnc.filter, 3)
[0, 0]
[1, 0]
[2, 0]
array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])
Fourier domain filters¶
The functions described in this section perform filtering
operations in the Fourier domain. Thus, the input array of such a
function should be compatible with an inverse Fourier transform
function, such as the functions from the numpy.fft module. We,
therefore, have to deal with arrays that may be the result of a real
or a complex Fourier transform. In the case of a real Fourier
transform, only half of the of the symmetric complex transform is
stored. Additionally, it needs to be known what the length of the
axis was that was transformed by the real fft. The functions
described here provide a parameter n that, in the case of a real
transform, must be equal to the length of the real transform axis
before transformation. If this parameter is less than zero, it is
assumed that the input array was the result of a complex Fourier
transform. The parameter axis can be used to indicate along which
axis the real transform was executed.
The
fourier_shiftfunction multiplies the input array with the multidimensional Fourier transform of a shift operation for the given shift. The shift parameter is a sequence of shifts for each dimension or a single value for all dimensions.The
fourier_gaussianfunction multiplies the input array with the multidimensional Fourier transform of a Gaussian filter with given standard deviations sigma. The sigma parameter is a sequence of values for each dimension or a single value for all dimensions.The
fourier_uniformfunction multiplies the input array with the multidimensional Fourier transform of a uniform filter with given sizes size. The size parameter is a sequence of values for each dimension or a single value for all dimensions.The
fourier_ellipsoidfunction multiplies the input array with the multidimensional Fourier transform of an elliptically-shaped filter with given sizes size. The size parameter is a sequence of values for each dimension or a single value for all dimensions. This function is only implemented for dimensions 1, 2, and 3.
Interpolation functions¶
This section describes various interpolation functions that are based on B-spline theory. A good introduction to B-splines can be found in 1 with detailed algorithms for image interpolation given in 5.
Spline pre-filters¶
Interpolation using splines of an order larger than 1 requires a
pre-filtering step. The interpolation functions described in section
Interpolation functions apply pre-filtering by calling
spline_filter, but they can be instructed not to do this by
setting the prefilter keyword equal to False. This is useful if more
than one interpolation operation is done on the same array. In this
case, it is more efficient to do the pre-filtering only once and use a
pre-filtered array as the input of the interpolation functions. The
following two functions implement the pre-filtering:
The
spline_filter1dfunction calculates a 1-D spline filter along the given axis. An output array can optionally be provided. The order of the spline must be larger than 1 and less than 6.The
spline_filterfunction calculates a multidimensional spline filter.Note
The multidimensional filter is implemented as a sequence of 1-D spline filters. The intermediate arrays are stored in the same data type as the output. Therefore, if an output with a limited precision is requested, the results may be imprecise because intermediate results may be stored with insufficient precision. This can be prevented by specifying a output type of high precision.
Interpolation boundary handling¶
The interpolation functions all employ spline interpolation to effect some type of geometric transformation of the input array. This requires a mapping of the output coordinates to the input coordinates, and therefore, the possibility arises that input values outside the boundaries may be needed. This problem is solved in the same way as described in Filter functions for the multidimensional filter functions. Therefore, these functions all support a mode parameter that determines how the boundaries are handled, and a cval parameter that gives a constant value in case that the ‘constant’ mode is used. The behavior of all modes, including at non-integer locations is illustrated below. Note the boundaries are not handled the same for all modes; reflect (aka grid-mirror) and grid-wrap involve symmetry or repetition about a point that is half way between image samples (dashed vertical lines) while modes mirror and wrap treat the image as if it’s extent ends exactly at the first and last sample point rather than 0.5 samples past it.
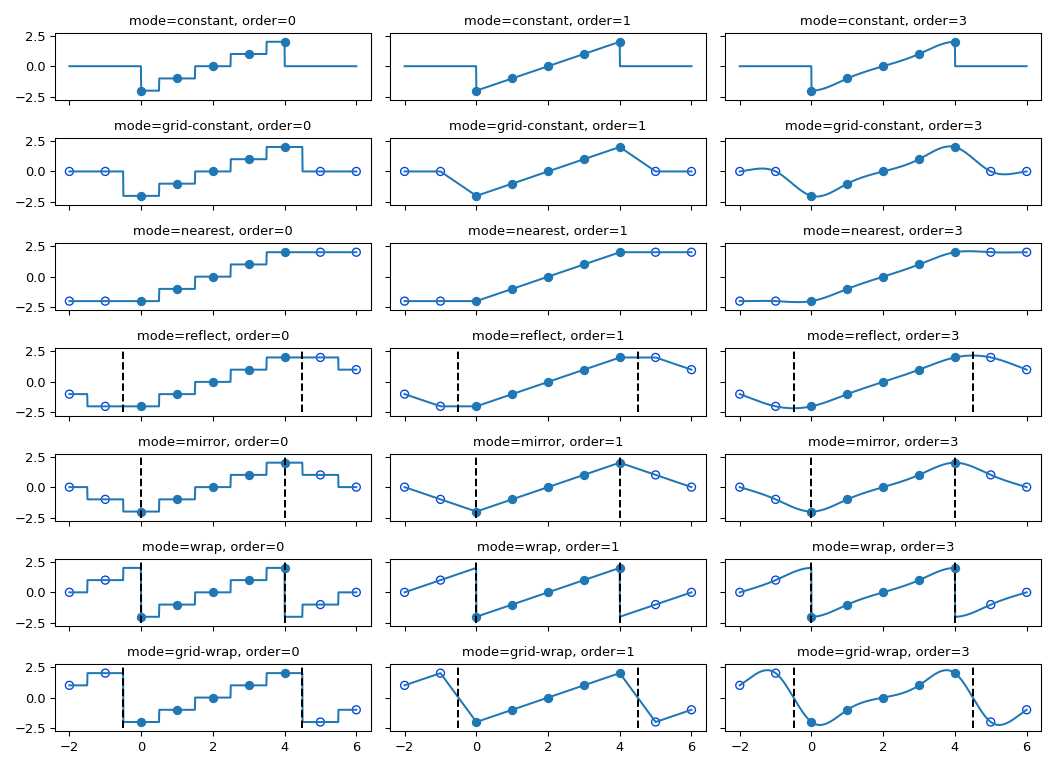
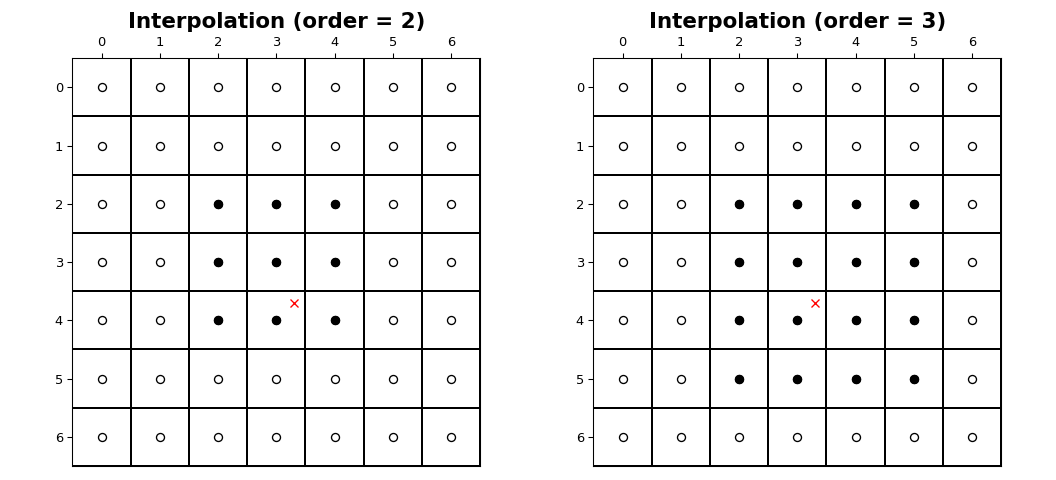
The coordinates of image samples fall on integer sampling locations
in the range from 0 to shape[i] - 1 along each axis, i. The figure
below illustrates the interpolation of a point at location (3.7, 3.3)
within an image of shape (7, 7). For an interpolation of order n,
n + 1 samples are involved along each axis. The filled circles
illustrate the sampling locations involved in the interpolation of the value at
the location of the red x.
Interpolation functions¶
The
geometric_transformfunction applies an arbitrary geometric transform to the input. The given mapping function is called at each point in the output to find the corresponding coordinates in the input. mapping must be a callable object that accepts a tuple of length equal to the output array rank and returns the corresponding input coordinates as a tuple of length equal to the input array rank. The output shape and output type can optionally be provided. If not given, they are equal to the input shape and type.For example:
>>> a = np.arange(12).reshape(4,3).astype(np.float64) >>> def shift_func(output_coordinates): ... return (output_coordinates[0] - 0.5, output_coordinates[1] - 0.5) ... >>> from scipy.ndimage import geometric_transform >>> geometric_transform(a, shift_func) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
Optionally, extra arguments can be defined and passed to the filter function. The extra_arguments and extra_keywords arguments can be used to pass a tuple of extra arguments and/or a dictionary of named arguments that are passed to derivative at each call. For example, we can pass the shifts in our example as arguments
>>> def shift_func(output_coordinates, s0, s1): ... return (output_coordinates[0] - s0, output_coordinates[1] - s1) ... >>> geometric_transform(a, shift_func, extra_arguments = (0.5, 0.5)) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
or
>>> geometric_transform(a, shift_func, extra_keywords = {'s0': 0.5, 's1': 0.5}) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
Note
The mapping function can also be written in C and passed using a
scipy.LowLevelCallable. See Extending scipy.ndimage in C for more information.The function
map_coordinatesapplies an arbitrary coordinate transformation using the given array of coordinates. The shape of the output is derived from that of the coordinate array by dropping the first axis. The parameter coordinates is used to find for each point in the output the corresponding coordinates in the input. The values of coordinates along the first axis are the coordinates in the input array at which the output value is found. (See also the numarray coordinates function.) Since the coordinates may be non- integer coordinates, the value of the input at these coordinates is determined by spline interpolation of the requested order.Here is an example that interpolates a 2D array at
(0.5, 0.5)and(1, 2):>>> a = np.arange(12).reshape(4,3).astype(np.float64) >>> a array([[ 0., 1., 2.], [ 3., 4., 5.], [ 6., 7., 8.], [ 9., 10., 11.]]) >>> from scipy.ndimage import map_coordinates >>> map_coordinates(a, [[0.5, 2], [0.5, 1]]) array([ 1.3625, 7.])
The
affine_transformfunction applies an affine transformation to the input array. The given transformation matrix and offset are used to find for each point in the output the corresponding coordinates in the input. The value of the input at the calculated coordinates is determined by spline interpolation of the requested order. The transformation matrix must be 2-D or can also be given as a 1-D sequence or array. In the latter case, it is assumed that the matrix is diagonal. A more efficient interpolation algorithm is then applied that exploits the separability of the problem. The output shape and output type can optionally be provided. If not given, they are equal to the input shape and type.The
shiftfunction returns a shifted version of the input, using spline interpolation of the requested order.The
zoomfunction returns a rescaled version of the input, using spline interpolation of the requested order.The
rotatefunction returns the input array rotated in the plane defined by the two axes given by the parameter axes, using spline interpolation of the requested order. The angle must be given in degrees. If reshape is true, then the size of the output array is adapted to contain the rotated input.
Morphology¶
Binary morphology¶
The
generate_binary_structurefunctions generates a binary structuring element for use in binary morphology operations. The rank of the structure must be provided. The size of the structure that is returned is equal to three in each direction. The value of each element is equal to one if the square of the Euclidean distance from the element to the center is less than or equal to connectivity. For instance, 2-D 4-connected and 8-connected structures are generated as follows:>>> from scipy.ndimage import generate_binary_structure >>> generate_binary_structure(2, 1) array([[False, True, False], [ True, True, True], [False, True, False]], dtype=bool) >>> generate_binary_structure(2, 2) array([[ True, True, True], [ True, True, True], [ True, True, True]], dtype=bool)
Most binary morphology functions can be expressed in terms of the basic operations erosion and dilation.
The
binary_erosionfunction implements binary erosion of arrays of arbitrary rank with the given structuring element. The origin parameter controls the placement of the structuring element, as described in Filter functions. If no structuring element is provided, an element with connectivity equal to one is generated usinggenerate_binary_structure. The border_value parameter gives the value of the array outside boundaries. The erosion is repeated iterations times. If iterations is less than one, the erosion is repeated until the result does not change anymore. If a mask array is given, only those elements with a true value at the corresponding mask element are modified at each iteration.The
binary_dilationfunction implements binary dilation of arrays of arbitrary rank with the given structuring element. The origin parameter controls the placement of the structuring element, as described in Filter functions. If no structuring element is provided, an element with connectivity equal to one is generated usinggenerate_binary_structure. The border_value parameter gives the value of the array outside boundaries. The dilation is repeated iterations times. If iterations is less than one, the dilation is repeated until the result does not change anymore. If a mask array is given, only those elements with a true value at the corresponding mask element are modified at each iteration.
Here is an example of using binary_dilation to find all elements
that touch the border, by repeatedly dilating an empty array from
the border using the data array as the mask:
>>> struct = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> a = np.array([[1,0,0,0,0], [1,1,0,1,0], [0,0,1,1,0], [0,0,0,0,0]])
>>> a
array([[1, 0, 0, 0, 0],
[1, 1, 0, 1, 0],
[0, 0, 1, 1, 0],
[0, 0, 0, 0, 0]])
>>> from scipy.ndimage import binary_dilation
>>> binary_dilation(np.zeros(a.shape), struct, -1, a, border_value=1)
array([[ True, False, False, False, False],
[ True, True, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False]], dtype=bool)
The binary_erosion and binary_dilation functions both
have an iterations parameter, which allows the erosion or dilation to
be repeated a number of times. Repeating an erosion or a dilation with
a given structure n times is equivalent to an erosion or a dilation
with a structure that is n-1 times dilated with itself. A function
is provided that allows the calculation of a structure that is dilated
a number of times with itself:
The
iterate_structurefunction returns a structure by dilation of the input structure iteration - 1 times with itself.For instance:
>>> struct = generate_binary_structure(2, 1) >>> struct array([[False, True, False], [ True, True, True], [False, True, False]], dtype=bool) >>> from scipy.ndimage import iterate_structure >>> iterate_structure(struct, 2) array([[False, False, True, False, False], [False, True, True, True, False], [ True, True, True, True, True], [False, True, True, True, False], [False, False, True, False, False]], dtype=bool) If the origin of the original structure is equal to 0, then it is also equal to 0 for the iterated structure. If not, the origin must also be adapted if the equivalent of the *iterations* erosions or dilations must be achieved with the iterated structure. The adapted origin is simply obtained by multiplying with the number of iterations. For convenience, the :func:`iterate_structure` also returns the adapted origin if the *origin* parameter is not ``None``: .. code:: python >>> iterate_structure(struct, 2, -1) (array([[False, False, True, False, False], [False, True, True, True, False], [ True, True, True, True, True], [False, True, True, True, False], [False, False, True, False, False]], dtype=bool), [-2, -2])
Other morphology operations can be defined in terms of erosion and dilation. The following functions provide a few of these operations for convenience:
The
binary_openingfunction implements binary opening of arrays of arbitrary rank with the given structuring element. Binary opening is equivalent to a binary erosion followed by a binary dilation with the same structuring element. The origin parameter controls the placement of the structuring element, as described in Filter functions. If no structuring element is provided, an element with connectivity equal to one is generated usinggenerate_binary_structure. The iterations parameter gives the number of erosions that is performed followed by the same number of dilations.The
binary_closingfunction implements binary closing of arrays of arbitrary rank with the given structuring element. Binary closing is equivalent to a binary dilation followed by a binary erosion with the same structuring element. The origin parameter controls the placement of the structuring element, as described in Filter functions. If no structuring element is provided, an element with connectivity equal to one is generated usinggenerate_binary_structure. The iterations parameter gives the number of dilations that is performed followed by the same number of erosions.The
binary_fill_holesfunction is used to close holes in objects in a binary image, where the structure defines the connectivity of the holes. The origin parameter controls the placement of the structuring element, as described in Filter functions. If no structuring element is provided, an element with connectivity equal to one is generated usinggenerate_binary_structure.The
binary_hit_or_missfunction implements a binary hit-or-miss transform of arrays of arbitrary rank with the given structuring elements. The hit-or-miss transform is calculated by erosion of the input with the first structure, erosion of the logical not of the input with the second structure, followed by the logical and of these two erosions. The origin parameters control the placement of the structuring elements, as described in Filter functions. If origin2 equalsNone, it is set equal to the origin1 parameter. If the first structuring element is not provided, a structuring element with connectivity equal to one is generated usinggenerate_binary_structure. If structure2 is not provided, it is set equal to the logical not of structure1.
Grey-scale morphology¶
Grey-scale morphology operations are the equivalents of binary morphology operations that operate on arrays with arbitrary values. Below, we describe the grey-scale equivalents of erosion, dilation, opening and closing. These operations are implemented in a similar fashion as the filters described in Filter functions, and we refer to this section for the description of filter kernels and footprints, and the handling of array borders. The grey-scale morphology operations optionally take a structure parameter that gives the values of the structuring element. If this parameter is not given, the structuring element is assumed to be flat with a value equal to zero. The shape of the structure can optionally be defined by the footprint parameter. If this parameter is not given, the structure is assumed to be rectangular, with sizes equal to the dimensions of the structure array, or by the size parameter if structure is not given. The size parameter is only used if both structure and footprint are not given, in which case the structuring element is assumed to be rectangular and flat with the dimensions given by size. The size parameter, if provided, must be a sequence of sizes or a single number in which case the size of the filter is assumed to be equal along each axis. The footprint parameter, if provided, must be an array that defines the shape of the kernel by its non-zero elements.
Similarly to binary erosion and dilation, there are operations for grey-scale erosion and dilation:
The
grey_erosionfunction calculates a multidimensional grey-scale erosion.The
grey_dilationfunction calculates a multidimensional grey-scale dilation.
Grey-scale opening and closing operations can be defined similarly to their binary counterparts:
The
grey_openingfunction implements grey-scale opening of arrays of arbitrary rank. Grey-scale opening is equivalent to a grey-scale erosion followed by a grey-scale dilation.The
grey_closingfunction implements grey-scale closing of arrays of arbitrary rank. Grey-scale opening is equivalent to a grey-scale dilation followed by a grey-scale erosion.The
morphological_gradientfunction implements a grey-scale morphological gradient of arrays of arbitrary rank. The grey-scale morphological gradient is equal to the difference of a grey-scale dilation and a grey-scale erosion.The
morphological_laplacefunction implements a grey-scale morphological laplace of arrays of arbitrary rank. The grey-scale morphological laplace is equal to the sum of a grey-scale dilation and a grey-scale erosion minus twice the input.The
white_tophatfunction implements a white top-hat filter of arrays of arbitrary rank. The white top-hat is equal to the difference of the input and a grey-scale opening.The
black_tophatfunction implements a black top-hat filter of arrays of arbitrary rank. The black top-hat is equal to the difference of a grey-scale closing and the input.
Distance transforms¶
Distance transforms are used to calculate the minimum distance from each element of an object to the background. The following functions implement distance transforms for three different distance metrics: Euclidean, city block, and chessboard distances.
The function
distance_transform_cdtuses a chamfer type algorithm to calculate the distance transform of the input, by replacing each object element (defined by values larger than zero) with the shortest distance to the background (all non-object elements). The structure determines the type of chamfering that is done. If the structure is equal to ‘cityblock’, a structure is generated usinggenerate_binary_structurewith a squared distance equal to 1. If the structure is equal to ‘chessboard’, a structure is generated usinggenerate_binary_structurewith a squared distance equal to the rank of the array. These choices correspond to the common interpretations of the city block and the chessboard distance metrics in two dimensions.In addition to the distance transform, the feature transform can be calculated. In this case, the index of the closest background element is returned along the first axis of the result. The return_distances, and return_indices flags can be used to indicate if the distance transform, the feature transform, or both must be returned.
The distances and indices arguments can be used to give optional output arrays that must be of the correct size and type (both
numpy.int32). The basics of the algorithm used to implement this function are described in 2.The function
distance_transform_edtcalculates the exact Euclidean distance transform of the input, by replacing each object element (defined by values larger than zero) with the shortest Euclidean distance to the background (all non-object elements).In addition to the distance transform, the feature transform can be calculated. In this case, the index of the closest background element is returned along the first axis of the result. The return_distances and return_indices flags can be used to indicate if the distance transform, the feature transform, or both must be returned.
Optionally, the sampling along each axis can be given by the sampling parameter, which should be a sequence of length equal to the input rank, or a single number in which the sampling is assumed to be equal along all axes.
The distances and indices arguments can be used to give optional output arrays that must be of the correct size and type (
numpy.float64andnumpy.int32).The algorithm used to implement this function is described in 3.The function
distance_transform_bfuses a brute-force algorithm to calculate the distance transform of the input, by replacing each object element (defined by values larger than zero) with the shortest distance to the background (all non-object elements). The metric must be one of “euclidean”, “cityblock”, or “chessboard”.In addition to the distance transform, the feature transform can be calculated. In this case, the index of the closest background element is returned along the first axis of the result. The return_distances and return_indices flags can be used to indicate if the distance transform, the feature transform, or both must be returned.
Optionally, the sampling along each axis can be given by the sampling parameter, which should be a sequence of length equal to the input rank, or a single number in which the sampling is assumed to be equal along all axes. This parameter is only used in the case of the Euclidean distance transform.
The distances and indices arguments can be used to give optional output arrays that must be of the correct size and type (
numpy.float64andnumpy.int32).Note
This function uses a slow brute-force algorithm, the function
distance_transform_cdtcan be used to more efficiently calculate city block and chessboard distance transforms. The functiondistance_transform_edtcan be used to more efficiently calculate the exact Euclidean distance transform.
Segmentation and labeling¶
Segmentation is the process of separating objects of interest from
the background. The most simple approach is, probably, intensity
thresholding, which is easily done with numpy functions:
>>> a = np.array([[1,2,2,1,1,0],
... [0,2,3,1,2,0],
... [1,1,1,3,3,2],
... [1,1,1,1,2,1]])
>>> np.where(a > 1, 1, 0)
array([[0, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0],
[0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 1, 0]])
The result is a binary image, in which the individual objects still
need to be identified and labeled. The function label
generates an array where each object is assigned a unique number:
The
labelfunction generates an array where the objects in the input are labeled with an integer index. It returns a tuple consisting of the array of object labels and the number of objects found, unless the output parameter is given, in which case only the number of objects is returned. The connectivity of the objects is defined by a structuring element. For instance, in 2D using a 4-connected structuring element gives:>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> s = [[0, 1, 0], [1,1,1], [0,1,0]] >>> from scipy.ndimage import label >>> label(a, s) (array([[0, 1, 1, 0, 0, 0], [0, 1, 1, 0, 2, 0], [0, 0, 0, 2, 2, 2], [0, 0, 0, 0, 2, 0]]), 2)
These two objects are not connected because there is no way in which we can place the structuring element, such that it overlaps with both objects. However, an 8-connected structuring element results in only a single object:
>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> s = [[1,1,1], [1,1,1], [1,1,1]] >>> label(a, s)[0] array([[0, 1, 1, 0, 0, 0], [0, 1, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0]])
If no structuring element is provided, one is generated by calling
generate_binary_structure(see Binary morphology) using a connectivity of one (which in 2D is the 4-connected structure of the first example). The input can be of any type, any value not equal to zero is taken to be part of an object. This is useful if you need to ‘re-label’ an array of object indices, for instance, after removing unwanted objects. Just apply the label function again to the index array. For instance:>>> l, n = label([1, 0, 1, 0, 1]) >>> l array([1, 0, 2, 0, 3]) >>> l = np.where(l != 2, l, 0) >>> l array([1, 0, 0, 0, 3]) >>> label(l)[0] array([1, 0, 0, 0, 2])
Note
The structuring element used by
labelis assumed to be symmetric.
There is a large number of other approaches for segmentation, for
instance, from an estimation of the borders of the objects that can be
obtained by derivative filters. One such approach is
watershed segmentation. The function watershed_ift generates
an array where each object is assigned a unique label, from an array
that localizes the object borders, generated, for instance, by a
gradient magnitude filter. It uses an array containing initial markers
for the objects:
The
watershed_iftfunction applies a watershed from markers algorithm, using an Iterative Forest Transform, as described in 4.The inputs of this function are the array to which the transform is applied, and an array of markers that designate the objects by a unique label, where any non-zero value is a marker. For instance:
>>> input = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 1, 1, 1, 1, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 0]], np.uint8) >>> markers = np.array([[1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0]], np.int8) >>> from scipy.ndimage import watershed_ift >>> watershed_ift(input, markers) array([[1, 1, 1, 1, 1, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 2, 2, 2, 2, 2, 1], [1, 2, 2, 2, 2, 2, 1], [1, 2, 2, 2, 2, 2, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1]], dtype=int8)
Here, two markers were used to designate an object (marker = 2) and the background (marker = 1). The order in which these are processed is arbitrary: moving the marker for the background to the lower-right corner of the array yields a different result:
>>> markers = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1]], np.int8) >>> watershed_ift(input, markers) array([[1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1]], dtype=int8)
The result is that the object (marker = 2) is smaller because the second marker was processed earlier. This may not be the desired effect if the first marker was supposed to designate a background object. Therefore,
watershed_ifttreats markers with a negative value explicitly as background markers and processes them after the normal markers. For instance, replacing the first marker by a negative marker gives a result similar to the first example:>>> markers = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, -1]], np.int8) >>> watershed_ift(input, markers) array([[-1, -1, -1, -1, -1, -1, -1], [-1, -1, 2, 2, 2, -1, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, -1, 2, 2, 2, -1, -1], [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)
The connectivity of the objects is defined by a structuring element. If no structuring element is provided, one is generated by calling
generate_binary_structure(see Binary morphology) using a connectivity of one (which in 2D is a 4-connected structure.) For example, using an 8-connected structure with the last example yields a different object:>>> watershed_ift(input, markers, ... structure = [[1,1,1], [1,1,1], [1,1,1]]) array([[-1, -1, -1, -1, -1, -1, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)
Note
The implementation of
watershed_iftlimits the data types of the input tonumpy.uint8andnumpy.uint16.
Object measurements¶
Given an array of labeled objects, the properties of the individual
objects can be measured. The find_objects function can be used
to generate a list of slices that for each object, give the
smallest sub-array that fully contains the object:
The
find_objectsfunction finds all objects in a labeled array and returns a list of slices that correspond to the smallest regions in the array that contains the object.For instance:
>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> l, n = label(a) >>> from scipy.ndimage import find_objects >>> f = find_objects(l) >>> a[f[0]] array([[1, 1], [1, 1]]) >>> a[f[1]] array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
The function
find_objectsreturns slices for all objects, unless the max_label parameter is larger then zero, in which case only the first max_label objects are returned. If an index is missing in the label array,Noneis return instead of a slice. For example:>>> from scipy.ndimage import find_objects >>> find_objects([1, 0, 3, 4], max_label = 3) [(slice(0, 1, None),), None, (slice(2, 3, None),)]
The list of slices generated by find_objects is useful to find
the position and dimensions of the objects in the array, but can also
be used to perform measurements on the individual objects. Say, we want
to find the sum of the intensities of an object in image:
>>> image = np.arange(4 * 6).reshape(4, 6)
>>> mask = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> labels = label(mask)[0]
>>> slices = find_objects(labels)
Then we can calculate the sum of the elements in the second object:
>>> np.where(labels[slices[1]] == 2, image[slices[1]], 0).sum()
80
That is, however, not particularly efficient and may also be more complicated for other types of measurements. Therefore, a few measurements functions are defined that accept the array of object labels and the index of the object to be measured. For instance, calculating the sum of the intensities can be done by:
>>> from scipy.ndimage import sum as ndi_sum
>>> ndi_sum(image, labels, 2)
80
For large arrays and small objects, it is more efficient to call the measurement functions after slicing the array:
>>> ndi_sum(image[slices[1]], labels[slices[1]], 2)
80
Alternatively, we can do the measurements for a number of labels with a single function call, returning a list of results. For instance, to measure the sum of the values of the background and the second object in our example, we give a list of labels:
>>> ndi_sum(image, labels, [0, 2])
array([178.0, 80.0])
The measurement functions described below all support the index
parameter to indicate which object(s) should be measured. The default
value of index is None. This indicates that all elements where the
label is larger than zero should be treated as a single object and
measured. Thus, in this case the labels array is treated as a mask
defined by the elements that are larger than zero. If index is a
number or a sequence of numbers it gives the labels of the objects
that are measured. If index is a sequence, a list of the results is
returned. Functions that return more than one result return their
result as a tuple if index is a single number, or as a tuple of
lists if index is a sequence.
The
sumfunction calculates the sum of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
meanfunction calculates the mean of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
variancefunction calculates the variance of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
standard_deviationfunction calculates the standard deviation of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
minimumfunction calculates the minimum of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
maximumfunction calculates the maximum of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
minimum_positionfunction calculates the position of the minimum of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
maximum_positionfunction calculates the position of the maximum of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
extremafunction calculates the minimum, the maximum, and their positions, of the elements of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation. The result is a tuple giving the minimum, the maximum, the position of the minimum, and the position of the maximum. The result is the same as a tuple formed by the results of the functions minimum, maximum, minimum_position, and maximum_position that are described above.The
center_of_massfunction calculates the center of mass of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation.The
histogramfunction calculates a histogram of the object with label(s) given by index, using the labels array for the object labels. If index isNone, all elements with a non-zero label value are treated as a single object. If label isNone, all elements of input are used in the calculation. Histograms are defined by their minimum (min), maximum (max), and the number of bins (bins). They are returned as 1-D arrays of typenumpy.int32.
Extending scipy.ndimage in C¶
A few functions in scipy.ndimage take a callback argument. This
can be either a python function or a scipy.LowLevelCallable containing a
pointer to a C function. Using a C function will generally be more
efficient, since it avoids the overhead of calling a python function on
many elements of an array. To use a C function, you must write a C
extension that contains the callback function and a Python function
that returns a scipy.LowLevelCallable containing a pointer to the
callback.
An example of a function that supports callbacks is
geometric_transform, which accepts a callback function that
defines a mapping from all output coordinates to corresponding
coordinates in the input array. Consider the following python example,
which uses geometric_transform to implement a shift function.
from scipy import ndimage
def transform(output_coordinates, shift):
input_coordinates = output_coordinates[0] - shift, output_coordinates[1] - shift
return input_coordinates
im = np.arange(12).reshape(4, 3).astype(np.float64)
shift = 0.5
print(ndimage.geometric_transform(im, transform, extra_arguments=(shift,)))
We can also implement the callback function with the following C code:
/* example.c */
#include <Python.h>
#include <numpy/npy_common.h>
static int
_transform(npy_intp *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data)
{
npy_intp i;
double shift = *(double *)user_data;
for (i = 0; i < input_rank; i++) {
input_coordinates[i] = output_coordinates[i] - shift;
}
return 1;
}
static char *transform_signature = "int (npy_intp *, double *, int, int, void *)";
static PyObject *
py_get_transform(PyObject *obj, PyObject *args)
{
if (!PyArg_ParseTuple(args, "")) return NULL;
return PyCapsule_New(_transform, transform_signature, NULL);
}
static PyMethodDef ExampleMethods[] = {
{"get_transform", (PyCFunction)py_get_transform, METH_VARARGS, ""},
{NULL, NULL, 0, NULL}
};
/* Initialize the module */
static struct PyModuleDef example = {
PyModuleDef_HEAD_INIT,
"example",
NULL,
-1,
ExampleMethods,
NULL,
NULL,
NULL,
NULL
};
PyMODINIT_FUNC
PyInit_example(void)
{
return PyModule_Create(&example);
}
More information on writing Python extension modules can be found
here. If the C code is in the file example.c, then it can be
compiled with the following setup.py,
from distutils.core import setup, Extension
import numpy
shift = Extension('example',
['example.c'],
include_dirs=[numpy.get_include()]
)
setup(name='example',
ext_modules=[shift]
)
and now running the script
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
from example import get_transform
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(get_transform(), ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
produces the same result as the original python script.
In the C version, _transform is the callback function and the
parameters output_coordinates and input_coordinates play the
same role as they do in the python version, while output_rank and
input_rank provide the equivalents of len(output_coordinates)
and len(input_coordinates). The variable shift is passed
through user_data instead of
extra_arguments. Finally, the C callback function returns an integer
status, which is one upon success and zero otherwise.
The function py_transform wraps the callback function in a
PyCapsule. The main steps are:
Initialize a
PyCapsule. The first argument is a pointer to the callback function.The second argument is the function signature, which must match exactly the one expected by
ndimage.Above, we used
scipy.LowLevelCallableto specifyuser_datathat we generated withctypes.A different approach would be to supply the data in the capsule context, that can be set by PyCapsule_SetContext and omit specifying
user_datainscipy.LowLevelCallable. However, in this approach we would need to deal with allocation/freeing of the data — freeing the data after the capsule has been destroyed can be done by specifying a non-NULL callback function in the third argument of PyCapsule_New.
C callback functions for ndimage all follow this scheme. The
next section lists the ndimage functions that accept a C
callback function and gives the prototype of the function.
See also
The functions that support low-level callback arguments are:
Below, we show alternative ways to write the code, using Numba, Cython, ctypes, or cffi instead of writing wrapper code in C.
Numba
Numba provides a way to write low-level functions easily in Python. We can write the above using Numba as:
# example.py
import numpy as np
import ctypes
from scipy import ndimage, LowLevelCallable
from numba import cfunc, types, carray
@cfunc(types.intc(types.CPointer(types.intp),
types.CPointer(types.double),
types.intc,
types.intc,
types.voidptr))
def transform(output_coordinates_ptr, input_coordinates_ptr,
output_rank, input_rank, user_data):
input_coordinates = carray(input_coordinates_ptr, (input_rank,))
output_coordinates = carray(output_coordinates_ptr, (output_rank,))
shift = carray(user_data, (1,), types.double)[0]
for i in range(input_rank):
input_coordinates[i] = output_coordinates[i] - shift
return 1
shift = 0.5
# Then call the function
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(transform.ctypes, ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
Cython
Functionally the same code as above can be written in Cython with somewhat less boilerplate as follows:
# example.pyx
from numpy cimport npy_intp as intp
cdef api int transform(intp *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data):
cdef intp i
cdef double shift = (<double *>user_data)[0]
for i in range(input_rank):
input_coordinates[i] = output_coordinates[i] - shift
return 1
# script.py
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
import example
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable.from_cython(example, "transform", ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
cffi
With cffi, you can interface with a C function residing in a shared library (DLL). First, we need to write the shared library, which we do in C — this example is for Linux/OSX:
/*
example.c
Needs to be compiled with "gcc -std=c99 -shared -fPIC -o example.so example.c"
or similar
*/
#include <stdint.h>
int
_transform(intptr_t *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data)
{
int i;
double shift = *(double *)user_data;
for (i = 0; i < input_rank; i++) {
input_coordinates[i] = output_coordinates[i] - shift;
}
return 1;
}
The Python code calling the library is:
import os
import numpy as np
from scipy import ndimage, LowLevelCallable
import cffi
# Construct the FFI object, and copypaste the function declaration
ffi = cffi.FFI()
ffi.cdef("""
int _transform(intptr_t *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data);
""")
# Open library
lib = ffi.dlopen(os.path.abspath("example.so"))
# Do the function call
user_data = ffi.new('double *', 0.5)
callback = LowLevelCallable(lib._transform, user_data)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
You can find more information in the cffi documentation.
ctypes
With ctypes, the C code and the compilation of the so/DLL is as for cffi above. The Python code is different:
# script.py
import os
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
lib = ctypes.CDLL(os.path.abspath('example.so'))
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
# Ctypes has no built-in intptr type, so override the signature
# instead of trying to get it via ctypes
callback = LowLevelCallable(lib._transform, ptr,
"int _transform(intptr_t *, double *, int, int, void *)")
# Perform the call
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
You can find more information in the ctypes documentation.
References¶
- 1
M. Unser, “Splines: A Perfect Fit for Signal and Image Processing,” IEEE Signal Processing Magazine, vol. 16, no. 6, pp. 22-38, November 1999.
- 2
G. Borgefors, “Distance transformations in arbitrary dimensions.”, Computer Vision, Graphics, and Image Processing, 27:321-345, 1984.
- 3
C. R. Maurer, Jr., R. Qi, and V. Raghavan, “A linear time algorithm for computing exact euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. PAMI 25, 265-270, 2003.
- 4
P. Felkel, R. Wegenkittl, and M. Bruckschwaiger, “Implementation and Complexity of the Watershed-from-Markers Algorithm Computed as a Minimal Cost Forest.”, Eurographics 2001, pp. C:26-35.
- 5
T. Briand and P. Monasse, “Theory and Practice of Image B-Spline Interpolation”, Image Processing On Line, 8, pp. 99–141, 2018. https://doi.org/10.5201/ipol.2018.221
