scipy.stats.invwishart#

scipy.stats.invwishart = <scipy.stats._multivariate.invwishart_gen object>[source]#

An inverse Wishart random variable.

The df keyword specifies the degrees of freedom. The scale keyword specifies the scale matrix, which must be symmetric and positive definite. In this context, the scale matrix is often interpreted in terms of a multivariate normal covariance matrix.

Parameters:

dfint: Degrees of freedom, must be greater than or equal to dimension of the scale matrix
scalearray_like: Symmetric positive definite scale matrix of the distribution
seed{None, int, np.random.RandomState, np.random.Generator}, optional: Used for drawing random variates. If seed is None, the RandomState singleton is used. If seed is an int, a new RandomState instance is used, seeded with seed. If seed is already a RandomState or Generator instance, then that object is used. Default is None.

Methods

pdf(x, df, scale)	Probability density function.
logpdf(x, df, scale)	Log of the probability density function.
rvs(df, scale, size=1, random_state=None)	Draw random samples from an inverse Wishart distribution.
entropy(df, scale)	Differential entropy of the distribution.

Raises:

scipy.linalg.LinAlgError: If the scale matrix scale is not positive definite.

See also

wishart

Notes

The scale matrix scale must be a symmetric positive definite matrix. Singular matrices, including the symmetric positive semi-definite case, are not supported. Symmetry is not checked; only the lower triangular portion is used.

The inverse Wishart distribution is often denoted

\[W_p^{-1}(\nu, \Psi)\]

where \(\nu\) is the degrees of freedom and \(\Psi\) is the \(p \times p\) scale matrix.

The probability density function for invwishart has support over positive definite matrices \(S\); if \(S \sim W^{-1}_p(\nu, \Sigma)\), then its PDF is given by:

\[f(S) = \frac{|\Sigma|^\frac{\nu}{2}}{2^{ \frac{\nu p}{2} } |S|^{\frac{\nu + p + 1}{2}} \Gamma_p \left(\frac{\nu}{2} \right)} \exp\left( -tr(\Sigma S^{-1}) / 2 \right)\]

If \(S \sim W_p^{-1}(\nu, \Psi)\) (inverse Wishart) then \(S^{-1} \sim W_p(\nu, \Psi^{-1})\) (Wishart).

If the scale matrix is 1-dimensional and equal to one, then the inverse Wishart distribution \(W_1(\nu, 1)\) collapses to the inverse Gamma distribution with parameters shape = \(\frac{\nu}{2}\) and scale = \(\frac{1}{2}\).

Instead of inverting a randomly generated Wishart matrix as described in [2], here the algorithm in [4] is used to directly generate a random inverse-Wishart matrix without inversion.

Added in version 0.16.0.

References

[1]

M.L. Eaton, “Multivariate Statistics: A Vector Space Approach”, Wiley, 1983.

[2]

M.C. Jones, “Generating Inverse Wishart Matrices”, Communications in Statistics - Simulation and Computation, vol. 14.2, pp.511-514, 1985.

[3]

Gupta, M. and Srivastava, S. “Parametric Bayesian Estimation of Differential Entropy and Relative Entropy”. Entropy 12, 818 - 843. 2010.

[4]

S.D. Axen, “Efficiently generating inverse-Wishart matrices and their Cholesky factors”, arXiv:2310.15884v1. 2023.

Examples

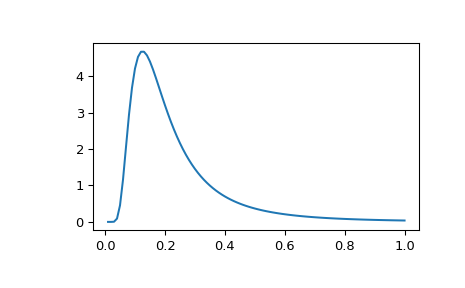
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import invwishart, invgamma
>>> x = np.linspace(0.01, 1, 100)
>>> iw = invwishart.pdf(x, df=6, scale=1)
>>> iw[:3]
array([  1.20546865e-15,   5.42497807e-06,   4.45813929e-03])
>>> ig = invgamma.pdf(x, 6/2., scale=1./2)
>>> ig[:3]
array([  1.20546865e-15,   5.42497807e-06,   4.45813929e-03])
>>> plt.plot(x, iw)
>>> plt.show()

../../_images/scipy-stats-invwishart-1_00_00.png

The input quantiles can be any shape of array, as long as the last axis labels the components.

Alternatively, the object may be called (as a function) to fix the degrees of freedom and scale parameters, returning a “frozen” inverse Wishart random variable:

>>> rv = invwishart(df=1, scale=1)
>>> # Frozen object with the same methods but holding the given
>>> # degrees of freedom and scale fixed.