scipy.special.voigt_profile#
- scipy.special.voigt_profile(x, sigma, gamma, out=None) = <ufunc 'voigt_profile'>#
Voigt profile.
The Voigt profile is a convolution of a 1-D Normal distribution with standard deviation
sigmaand a 1-D Cauchy distribution with half-width at half-maximumgamma.If
sigma = 0, PDF of Cauchy distribution is returned. Conversely, ifgamma = 0, PDF of Normal distribution is returned. Ifsigma = gamma = 0, the return value isInfforx = 0, and0for all otherx.- Parameters:
- xarray_like
Real argument
- sigmaarray_like
The standard deviation of the Normal distribution part
- gammaarray_like
The half-width at half-maximum of the Cauchy distribution part
- outndarray, optional
Optional output array for the function values
- Returns:
- scalar or ndarray
The Voigt profile at the given arguments
See also
wofzFaddeeva function
Notes
It can be expressed in terms of Faddeeva function
\[V(x; \sigma, \gamma) = \frac{Re[w(z)]}{\sigma\sqrt{2\pi}},\]\[z = \frac{x + i\gamma}{\sqrt{2}\sigma}\]where \(w(z)\) is the Faddeeva function.
References
Examples
Calculate the function at point 2 for
sigma=1andgamma=1.>>> from scipy.special import voigt_profile >>> import numpy as np >>> import matplotlib.pyplot as plt >>> voigt_profile(2, 1., 1.) 0.09071519942627544
Calculate the function at several points by providing a NumPy array for x.
>>> values = np.array([-2., 0., 5]) >>> voigt_profile(values, 1., 1.) array([0.0907152 , 0.20870928, 0.01388492])
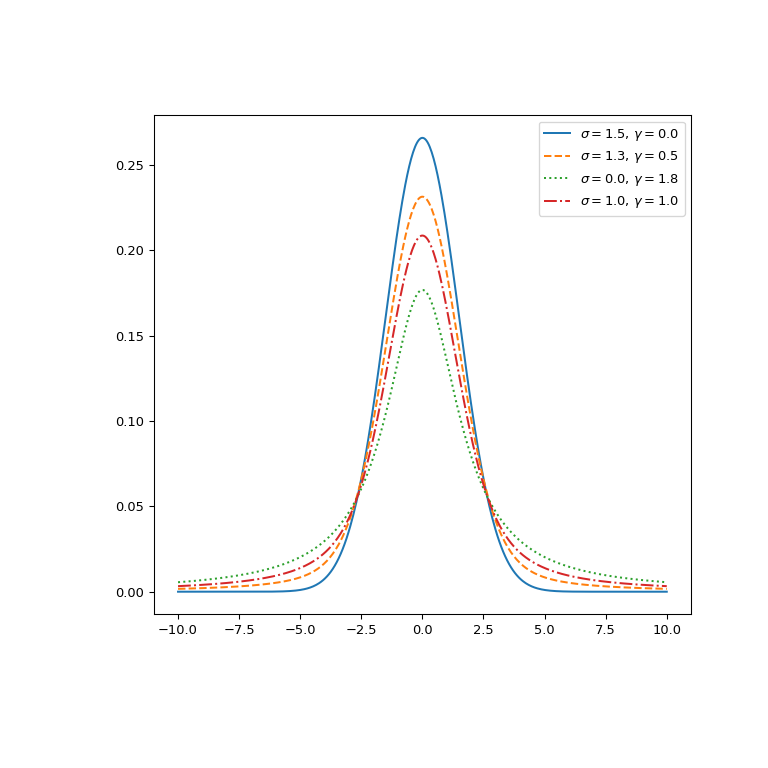
Plot the function for different parameter sets.
>>> fig, ax = plt.subplots(figsize=(8, 8)) >>> x = np.linspace(-10, 10, 500) >>> parameters_list = [(1.5, 0., "solid"), (1.3, 0.5, "dashed"), ... (0., 1.8, "dotted"), (1., 1., "dashdot")] >>> for params in parameters_list: ... sigma, gamma, linestyle = params ... voigt = voigt_profile(x, sigma, gamma) ... ax.plot(x, voigt, label=rf"$\sigma={sigma},\, \gamma={gamma}$", ... ls=linestyle) >>> ax.legend() >>> plt.show()
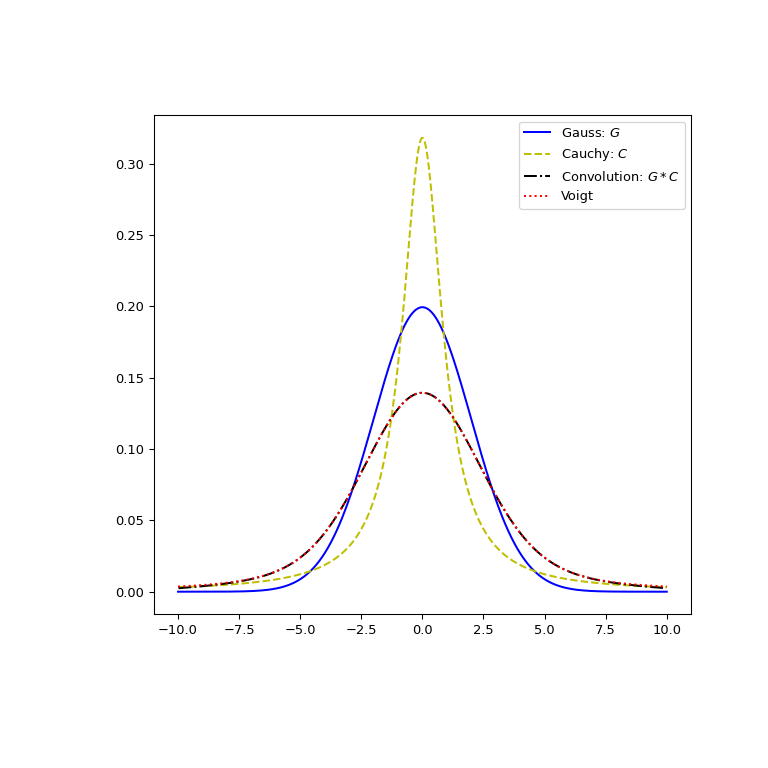
Verify visually that the Voigt profile indeed arises as the convolution of a normal and a Cauchy distribution.
>>> from scipy.signal import convolve >>> x, dx = np.linspace(-10, 10, 500, retstep=True) >>> def gaussian(x, sigma): ... return np.exp(-0.5 * x**2/sigma**2)/(sigma * np.sqrt(2*np.pi)) >>> def cauchy(x, gamma): ... return gamma/(np.pi * (np.square(x)+gamma**2)) >>> sigma = 2 >>> gamma = 1 >>> gauss_profile = gaussian(x, sigma) >>> cauchy_profile = cauchy(x, gamma) >>> convolved = dx * convolve(cauchy_profile, gauss_profile, mode="same") >>> voigt = voigt_profile(x, sigma, gamma) >>> fig, ax = plt.subplots(figsize=(8, 8)) >>> ax.plot(x, gauss_profile, label="Gauss: $G$", c='b') >>> ax.plot(x, cauchy_profile, label="Cauchy: $C$", c='y', ls="dashed") >>> xx = 0.5*(x[1:] + x[:-1]) # midpoints >>> ax.plot(xx, convolved[1:], label="Convolution: $G * C$", ls='dashdot', ... c='k') >>> ax.plot(x, voigt, label="Voigt", ls='dotted', c='r') >>> ax.legend() >>> plt.show()