scipy.special.besselpoly#
- scipy.special.besselpoly(a, lmb, nu, out=None) = <ufunc 'besselpoly'>#
Weighted integral of the Bessel function of the first kind.
Computes
\[\int_0^1 x^\lambda J_\nu(2 a x) \, dx\]where \(J_\nu\) is a Bessel function and \(\lambda=lmb\), \(\nu=nu\).
- Parameters:
- aarray_like
Scale factor inside the Bessel function.
- lmbarray_like
Power of x
- nuarray_like
Order of the Bessel function.
- outndarray, optional
Optional output array for the function results.
- Returns:
- scalar or ndarray
Value of the integral.
References
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Examples
Evaluate the function for one parameter set.
>>> from scipy.special import besselpoly >>> besselpoly(1, 1, 1) 0.24449718372863877
Evaluate the function for different scale factors.
>>> import numpy as np >>> factors = np.array([0., 3., 6.]) >>> besselpoly(factors, 1, 1) array([ 0. , -0.00549029, 0.00140174])
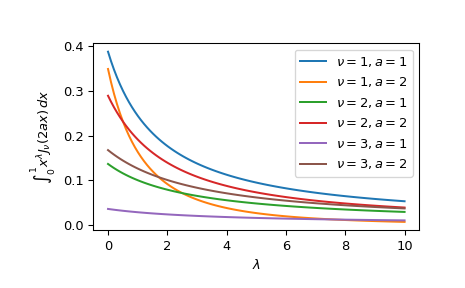
Plot the function for varying powers, orders and scales.
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> powers = np.linspace(0, 10, 100) >>> orders = [1, 2, 3] >>> scales = [1, 2] >>> all_combinations = [(order, scale) for order in orders ... for scale in scales] >>> for order, scale in all_combinations: ... ax.plot(powers, besselpoly(scale, powers, order), ... label=rf"$\nu={order}, a={scale}$") >>> ax.legend() >>> ax.set_xlabel(r"$\lambda$") >>> ax.set_ylabel(r"$\int_0^1 x^{\lambda} J_{\nu}(2ax)\,dx$") >>> plt.show()