bracket#
- scipy.optimize.bracket(func, xa=0.0, xb=1.0, args=(), grow_limit=110.0, maxiter=1000)[source]#
Bracket the minimum of a function.
Given a function and distinct initial points, search in the downhill direction (as defined by the initial points) and return three points that bracket the minimum of the function.
- Parameters:
- funccallable f(x,*args)
Objective function to minimize.
- xa, xbfloat, optional
Initial points. Defaults xa to 0.0, and xb to 1.0. A local minimum need not be contained within this interval.
- argstuple, optional
Additional arguments (if present), passed to func.
- grow_limitfloat, optional
Maximum grow limit. Defaults to 110.0
- maxiterint, optional
Maximum number of iterations to perform. Defaults to 1000.
- Returns:
- xa, xb, xcfloat
Final points of the bracket.
- fa, fb, fcfloat
Objective function values at the bracket points.
- funcallsint
Number of function evaluations made.
- Raises:
- BracketError
If no valid bracket is found before the algorithm terminates. See notes for conditions of a valid bracket.
Notes
The algorithm attempts to find three strictly ordered points (i.e. \(x_a < x_b < x_c\) or \(x_c < x_b < x_a\)) satisfying \(f(x_b) ≤ f(x_a)\) and \(f(x_b) ≤ f(x_c)\), where one of the inequalities must be satistfied strictly and all \(x_i\) must be finite.
Examples
This function can find a downward convex region of a function:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.optimize import bracket >>> def f(x): ... return 10*x**2 + 3*x + 5 >>> x = np.linspace(-2, 2) >>> y = f(x) >>> init_xa, init_xb = 0.1, 1 >>> xa, xb, xc, fa, fb, fc, funcalls = bracket(f, xa=init_xa, xb=init_xb) >>> plt.axvline(x=init_xa, color="k", linestyle="--") >>> plt.axvline(x=init_xb, color="k", linestyle="--") >>> plt.plot(x, y, "-k") >>> plt.plot(xa, fa, "bx") >>> plt.plot(xb, fb, "rx") >>> plt.plot(xc, fc, "bx") >>> plt.show()
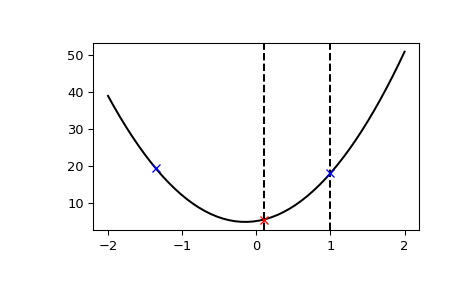
Note that both initial points were to the right of the minimum, and the third point was found in the “downhill” direction: the direction in which the function appeared to be decreasing (to the left). The final points are strictly ordered, and the function value at the middle point is less than the function values at the endpoints; it follows that a minimum must lie within the bracket.