scipy.stats.

yeojohnson_llf

scipy.stats.yeojohnson_llf(lmb, data)

The yeojohnson log-likelihood function.

Parameters:

lmbscalar

Parameter for Yeo-Johnson transformation. See yeojohnson for details.

dataarray_like

Data to calculate Yeo-Johnson log-likelihood for. If data is multi-dimensional, the log-likelihood is calculated along the first axis.

Returns:

llffloat

Yeo-Johnson log-likelihood of data given lmb.

See also

yeojohnson, probplot, yeojohnson_normplot, yeojohnson_normmax

Notes

The Yeo-Johnson log-likelihood function is defined here as

\[llf = -N/2 \log(\hat{\sigma}^2) + (\lambda - 1) \sum_i \text{ sign }(x_i)\log(|x_i| + 1)\]

where \(\hat{\sigma}^2\) is estimated variance of the Yeo-Johnson transformed input data x.

Added in version 1.2.0.

Examples

Try it in your browser!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes

Generate some random variates and calculate Yeo-Johnson log-likelihood values for them for a range of lmbda values:

>>> x = stats.loggamma.rvs(5, loc=10, size=1000)
>>> lmbdas = np.linspace(-2, 10)
>>> llf = np.zeros(lmbdas.shape, dtype=float)
>>> for ii, lmbda in enumerate(lmbdas):
...     llf[ii] = stats.yeojohnson_llf(lmbda, x)

Also find the optimal lmbda value with yeojohnson:

>>> x_most_normal, lmbda_optimal = stats.yeojohnson(x)

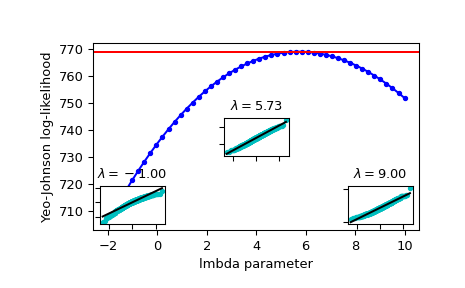
Plot the log-likelihood as function of lmbda. Add the optimal lmbda as a horizontal line to check that that’s really the optimum:

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(lmbdas, llf, 'b.-')
>>> ax.axhline(stats.yeojohnson_llf(lmbda_optimal, x), color='r')
>>> ax.set_xlabel('lmbda parameter')
>>> ax.set_ylabel('Yeo-Johnson log-likelihood')

Now add some probability plots to show that where the log-likelihood is maximized the data transformed with yeojohnson looks closest to normal:

>>> locs = [3, 10, 4]  # 'lower left', 'center', 'lower right'
>>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs):
...     xt = stats.yeojohnson(x, lmbda=lmbda)
...     (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt)
...     ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc)
...     ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-')
...     ax_inset.set_xticklabels([])
...     ax_inset.set_yticklabels([])
...     ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)

>>> plt.show()

Go BackOpen In Tab