scipy.stats.qmc.

MultivariateNormalQMC

class scipy.stats.qmc.MultivariateNormalQMC(mean, cov=None, *, cov_root=None, inv_transform=True, engine=None, seed=None)

QMC sampling from a multivariate Normal \(N(\mu, \Sigma)\).

Parameters:

meanarray_like (d,)

The mean vector. Where d is the dimension.

covarray_like (d, d), optional

The covariance matrix. If omitted, use cov_root instead. If both cov and cov_root are omitted, use the identity matrix.

cov_rootarray_like (d, d’), optional

A root decomposition of the covariance matrix, where d' may be less than d if the covariance is not full rank. If omitted, use cov.

inv_transformbool, optional

If True, use inverse transform instead of Box-Muller. Default is True.

engineQMCEngine, optional

Quasi-Monte Carlo engine sampler. If None, Sobol is used.

seed{None, int, numpy.random.Generator}, optional

Used only if engine is None. If seed is an int or None, a new numpy.random.Generator is created using np.random.default_rng(seed). If seed is already a Generator instance, then the provided instance is used.

Methods

random([n])

Draw n QMC samples from the multivariate Normal.

Examples

Try it in your browser!

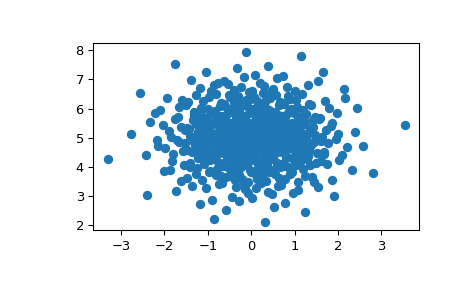
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import qmc
>>> dist = qmc.MultivariateNormalQMC(mean=[0, 5], cov=[[1, 0], [0, 1]])
>>> sample = dist.random(512)
>>> _ = plt.scatter(sample[:, 0], sample[:, 1])
>>> plt.show()

Go BackOpen In Tab