gaussian_kde#
- class scipy.stats.gaussian_kde(dataset, bw_method=None, weights=None)[source]#
Representation of a kernel-density estimate using Gaussian kernels.
Kernel density estimation is a way to estimate the probability density function (PDF) of a random variable in a non-parametric way.
gaussian_kdeworks for both uni-variate and multi-variate data. It includes automatic bandwidth determination. The estimation works best for a unimodal distribution; bimodal or multi-modal distributions tend to be oversmoothed.- Parameters:
- datasetarray_like
Datapoints to estimate from. In case of univariate data this is a 1-D array, otherwise a 2-D array with shape (# of dims, # of data).
- bw_methodstr, scalar or callable, optional
The method used to calculate the bandwidth factor. This can be ‘scott’, ‘silverman’, a scalar constant or a callable. If a scalar, this will be used directly as factor. If a callable, it should take a
gaussian_kdeinstance as only parameter and return a scalar. If None (default), ‘scott’ is used. See Notes for more details.- weightsarray_like, optional
weights of datapoints. This must be the same shape as dataset. If None (default), the samples are assumed to be equally weighted
- Attributes:
- datasetndarray
The dataset with which
gaussian_kdewas initialized.- dint
Number of dimensions.
- nint
Number of datapoints.
- neffint
Effective number of datapoints.
Added in version 1.2.0.
- factorfloat
The bandwidth factor obtained from
covariance_factor.- covariancendarray
The kernel covariance matrix; this is the data covariance matrix multiplied by the square of the bandwidth factor, e.g.
np.cov(dataset) * factor**2.- inv_covndarray
The inverse of covariance.
Methods
evaluate(points)Evaluate the estimated pdf on a set of points.
__call__(points)Evaluate the estimated pdf on a set of points.
integrate_gaussian(mean, cov)Multiply estimated density by a multivariate Gaussian and integrate over the whole space.
integrate_box_1d(low, high)Computes the integral of a 1D pdf between two bounds.
integrate_box(low_bounds, high_bounds[, ...])Computes the integral of a pdf over a rectangular interval.
integrate_kde(other)Computes the integral of the product of this kernel density estimate with another.
pdf(x)Evaluate the estimated pdf on a provided set of points.
logpdf(x)Evaluate the log of the estimated pdf on a provided set of points.
resample([size, seed])Randomly sample a dataset from the estimated pdf.
set_bandwidth([bw_method])Compute the bandwidth factor with given method.
Computes the bandwidth factor factor.
marginal(dimensions)Return a marginal KDE distribution
Notes
Bandwidth selection strongly influences the estimate obtained from the KDE (much more so than the actual shape of the kernel). Bandwidth selection can be done by a “rule of thumb”, by cross-validation, by “plug-in methods” or by other means; see [3], [4] for reviews.
gaussian_kdeuses a rule of thumb, the default is Scott’s Rule.Scott’s Rule [1], implemented as
scotts_factor, is:n**(-1./(d+4)),
with
nthe number of data points anddthe number of dimensions. In the case of unequally weighted points,scotts_factorbecomes:neff**(-1./(d+4)),
with
neffthe effective number of datapoints. Silverman’s suggestion for multivariate data [2], implemented assilverman_factor, is:(n * (d + 2) / 4.)**(-1. / (d + 4)).
or in the case of unequally weighted points:
(neff * (d + 2) / 4.)**(-1. / (d + 4)).
Note that this is not the same as “Silverman’s rule of thumb” [6], which may be more robust in the univariate case; see documentation of the
set_bandwidthmethod for implementing a custom bandwidth rule.Good general descriptions of kernel density estimation can be found in [1] and [2], the mathematics for this multi-dimensional implementation can be found in [1].
With a set of weighted samples, the effective number of datapoints
neffis defined by:neff = sum(weights)^2 / sum(weights^2)
as detailed in [5].
gaussian_kdedoes not currently support data that lies in a lower-dimensional subspace of the space in which it is expressed. For such data, consider performing principal component analysis / dimensionality reduction and usinggaussian_kdewith the transformed data.References
[1] (1,2,3)D.W. Scott, “Multivariate Density Estimation: Theory, Practice, and Visualization”, John Wiley & Sons, New York, Chicester, 1992.
[2] (1,2)B.W. Silverman, “Density Estimation for Statistics and Data Analysis”, Vol. 26, Monographs on Statistics and Applied Probability, Chapman and Hall, London, 1986.
[3]B.A. Turlach, “Bandwidth Selection in Kernel Density Estimation: A Review”, CORE and Institut de Statistique, Vol. 19, pp. 1-33, 1993.
[4]D.M. Bashtannyk and R.J. Hyndman, “Bandwidth selection for kernel conditional density estimation”, Computational Statistics & Data Analysis, Vol. 36, pp. 279-298, 2001.
[5]Gray P. G., 1969, Journal of the Royal Statistical Society. Series A (General), 132, 272
[6]Kernel density estimation. Wikipedia. https://en.wikipedia.org/wiki/Kernel_density_estimation
Examples
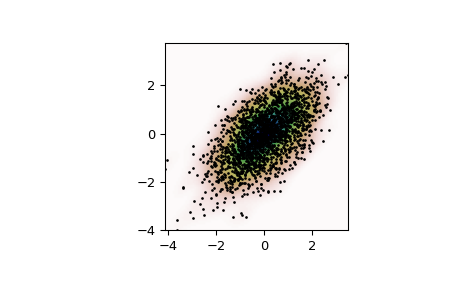
Generate some random two-dimensional data:
>>> import numpy as np >>> from scipy import stats >>> def measure(n): ... "Measurement model, return two coupled measurements." ... m1 = np.random.normal(size=n) ... m2 = np.random.normal(scale=0.5, size=n) ... return m1+m2, m1-m2
>>> m1, m2 = measure(2000) >>> xmin = m1.min() >>> xmax = m1.max() >>> ymin = m2.min() >>> ymax = m2.max()
Perform a kernel density estimate on the data:
>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j] >>> positions = np.vstack([X.ravel(), Y.ravel()]) >>> values = np.vstack([m1, m2]) >>> kernel = stats.gaussian_kde(values) >>> Z = np.reshape(kernel(positions).T, X.shape)
Plot the results:
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r, ... extent=[xmin, xmax, ymin, ymax]) >>> ax.plot(m1, m2, 'k.', markersize=2) >>> ax.set_xlim([xmin, xmax]) >>> ax.set_ylim([ymin, ymax]) >>> plt.show()
Compare against manual KDE at a point:
>>> point = [1, 2] >>> mean = values.T >>> cov = kernel.factor**2 * np.cov(values) >>> X = stats.multivariate_normal(cov=cov) >>> res = kernel.pdf(point) >>> ref = X.pdf(point - mean).sum() / len(mean) >>> np.allclose(res, ref) True