scipy.special.y1#

scipy.special.y1(x, out=None) = <ufunc 'y1'>#

Bessel function of the second kind of order 1.

Parameters:

xarray_like: Argument (float).
outndarray, optional: Optional output array for the function results

Returns:

Yscalar or ndarray: Value of the Bessel function of the second kind of order 1 at x.

See also

j1: Bessel function of the first kind of order 1
yn: Bessel function of the second kind
yv: Bessel function of the second kind

Notes

The domain is divided into the intervals [0, 8] and (8, infinity). In the first interval a 25 term Chebyshev expansion is used, and computing \(J_1\) (the Bessel function of the first kind) is required. In the second, the asymptotic trigonometric representation is employed using two rational functions of degree 5/5.

This function is a wrapper for the Cephes [1] routine y1.

References

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Examples

Calculate the function at one point:

>>> from scipy.special import y1
>>> y1(1.)
-0.7812128213002888

Calculate at several points:

>>> import numpy as np
>>> y1(np.array([0.5, 2., 3.]))
array([-1.47147239, -0.10703243,  0.32467442])

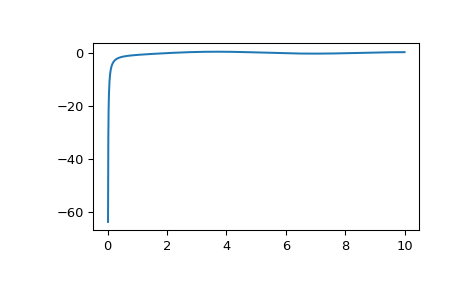
Plot the function from 0 to 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 10., 1000)
>>> y = y1(x)
>>> ax.plot(x, y)
>>> plt.show()