unit_impulse#
- scipy.signal.unit_impulse(shape, idx=None, dtype=<class 'float'>)[source]#
Unit impulse signal (discrete delta function) or unit basis vector.
- Parameters:
- shapeint or tuple of int
Number of samples in the output (1-D), or a tuple that represents the shape of the output (N-D).
- idxNone or int or tuple of int or ‘mid’, optional
Index at which the value is 1. If None, defaults to the 0th element. If
idx='mid', the impulse will be centered atshape // 2in all dimensions. If an int, the impulse will be at idx in all dimensions.- dtypedata-type, optional
The desired data-type for the array, e.g.,
numpy.int8. Default isnumpy.float64.
- Returns:
- yndarray
Output array containing an impulse signal.
Notes
In digital signal processing literature the unit impulse signal is often represented by the Kronecker delta. [1] I.e., a signal \(u_k[n]\), which is zero everywhere except being one at the \(k\)-th sample, can be expressed as
\[u_k[n] = \delta[n-k] \equiv \delta_{n,k}\ .\]Furthermore, the unit impulse is frequently interpreted as the discrete-time version of the continuous-time Dirac distribution. [2]
Array API Standard Support
unit_impulsehas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
⛔
⛔
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
References
[1]“Kronecker delta”, Wikipedia, https://en.wikipedia.org/wiki/Kronecker_delta#Digital_signal_processing
[2]“Dirac delta function” Wikipedia, https://en.wikipedia.org/wiki/Dirac_delta_function#Relationship_to_the_Kronecker_delta
Added in version 0.19.0.
Examples
An impulse at the 0th element (\(\\delta[n]\)):
>>> from scipy import signal >>> signal.unit_impulse(8) array([ 1., 0., 0., 0., 0., 0., 0., 0.])
Impulse offset by 2 samples (\(\\delta[n-2]\)):
>>> signal.unit_impulse(7, 2) array([ 0., 0., 1., 0., 0., 0., 0.])
2-dimensional impulse, centered:
>>> signal.unit_impulse((3, 3), 'mid') array([[ 0., 0., 0.], [ 0., 1., 0.], [ 0., 0., 0.]])
Impulse at (2, 2), using broadcasting:
>>> signal.unit_impulse((4, 4), 2) array([[ 0., 0., 0., 0.], [ 0., 0., 0., 0.], [ 0., 0., 1., 0.], [ 0., 0., 0., 0.]])
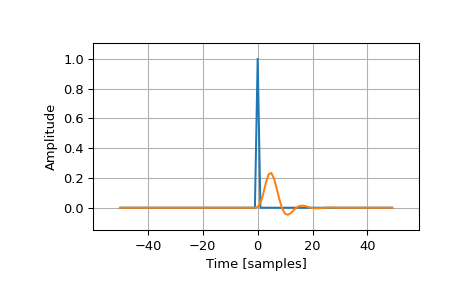
Plot the impulse response of a 4th-order Butterworth lowpass filter:
>>> imp = signal.unit_impulse(100, 'mid') >>> b, a = signal.butter(4, 0.2) >>> response = signal.lfilter(b, a, imp)
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> plt.plot(np.arange(-50, 50), imp) >>> plt.plot(np.arange(-50, 50), response) >>> plt.margins(0.1, 0.1) >>> plt.xlabel('Time [samples]') >>> plt.ylabel('Amplitude') >>> plt.grid(True) >>> plt.show()