qspline1d_eval#
- scipy.signal.qspline1d_eval(cj, newx, dx=1.0, x0=0)[source]#
Evaluate a quadratic spline at the new set of points.
- Parameters:
- cjndarray
Quadratic spline coefficients
- newxndarray
New set of points.
- dxfloat, optional
Old sample-spacing, the default value is 1.0.
- x0int, optional
Old origin, the default value is 0.
- Returns:
- resndarray
Evaluated a quadratic spline points.
See also
qspline1dCompute quadratic spline coefficients for rank-1 array.
Notes
dx is the old sample-spacing while x0 was the old origin. In other-words the old-sample points (knot-points) for which the cj represent spline coefficients were at equally-spaced points of:
oldx = x0 + j*dx j=0...N-1, with N=len(cj)
Edges are handled using mirror-symmetric boundary conditions.
Array API Standard Support
qspline1d_evalhas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
⛔
JAX
⚠️ no JIT
⛔
Dask
⚠️ computes graph
n/a
See Support for the array API standard for more information.
Examples
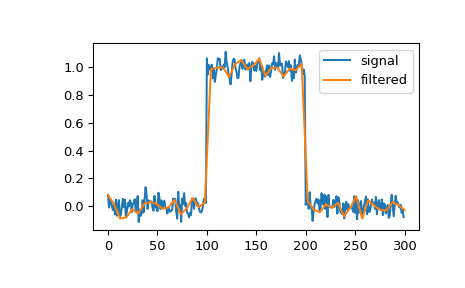
We can filter a signal to reduce and smooth out high-frequency noise with a quadratic spline:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.signal import qspline1d, qspline1d_eval >>> rng = np.random.default_rng() >>> sig = np.repeat([0., 1., 0.], 100) >>> sig += rng.standard_normal(len(sig))*0.05 # add noise >>> time = np.linspace(0, len(sig)) >>> filtered = qspline1d_eval(qspline1d(sig), time) >>> plt.plot(sig, label="signal") >>> plt.plot(time, filtered, label="filtered") >>> plt.legend() >>> plt.show()