FloaterHormannInterpolator#
- class scipy.interpolate.FloaterHormannInterpolator(points, values, *, d=3, axis=0)[source]#
Floater-Hormann barycentric rational interpolator (C∞ smooth on real axis).
As described in [1], the method of Floater and Hormann computes weights for a barycentric rational interpolant with no poles on the real axis.
- Parameters:
- x1D array_like, shape (n,)
1-D array containing values of the independent variable. Values may be real or complex but must be finite.
- yarray_like, shape (n, …)
Array containing values of the dependent variable. Infinite and NaN values of y and corresponding values of x will be discarded.
- dint, default: 3
Integer satisfying
0 <= d < n. Floater-Hormann interpolation blendsn - dpolynomials of degree d together; ford = n - 1, this is equivalent to polynomial interpolation.- axisint, default: 0
Axis of y corresponding to x.
- Attributes:
- weightsarray
Weights of the barycentric approximation.
Methods
__call__(z)Evaluate the rational approximation at given values.
poles()Compute the poles of the rational approximation.
residues()Compute the residues of the poles of the approximation.
roots()Compute the roots of the rational approximation.
See also
Notes
The Floater-Hormann interpolant is a rational function that interpolates the data with approximation order \(O(h^{d+1})\). The rational function blends
n - dpolynomials of degree d together to produce a rational interpolant that contains no poles on the real axis, unlikeAAA. The interpolant is given by\[r(x) = \frac{\sum_{i=0}^{n-d} \lambda_i(x) p_i(x)} {\sum_{i=0}^{n-d} \lambda_i(x)},\]where \(p_i(x)\) is an interpolating polynomial of at most degree d through the points \((x_i,y_i),\dots,(x_{i+d},y_{i+d})\), and \(\lambda_i(z)\) are blending functions defined by
\[\lambda_i(x) = \frac{(-1)^i}{(x - x_i)\cdots(x - x_{i+d})}.\]When
d = n - 1this reduces to polynomial interpolation.Due to its stability, the following barycentric representation of the above equation is used for computation
\[r(z) = \frac{\sum_{k=1}^m\ w_k f_k / (x - x_k)}{\sum_{k=1}^m w_k / (x - x_k)},\]where the weights \(w_j\) are computed as
\[\begin{split}w_k &= (-1)^{k - d} \sum_{i \in J_k} \prod_{j = i, j \neq k}^{i + d} 1/|x_k - x_j|, \\ J_k &= \{ i \in I: k - d \leq i \leq k\},\\ I &= \{0, 1, \dots, n - d\}.\end{split}\]References
[1]M.S. Floater and K. Hormann, “Barycentric rational interpolation with no poles and high rates of approximation”, Numer. Math. 107, 315 (2007). DOI:10.1007/s00211-007-0093-y
Examples
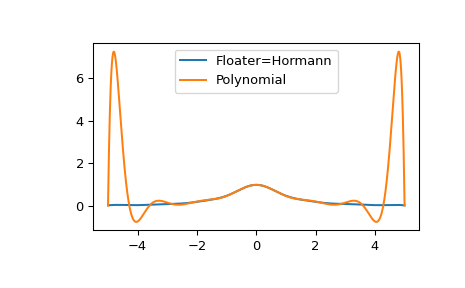
Here we compare the method against polynomial interpolation for an example where the polynomial interpolation fails due to Runge’s phenomenon.
>>> import numpy as np >>> from scipy.interpolate import (FloaterHormannInterpolator, ... BarycentricInterpolator) >>> def f(x): ... return 1/(1 + x**2) >>> x = np.linspace(-5, 5, num=15) >>> r = FloaterHormannInterpolator(x, f(x)) >>> p = BarycentricInterpolator(x, f(x)) >>> xx = np.linspace(-5, 5, num=1000) >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.plot(xx, f(xx), label="f(x)") >>> ax.plot(xx, r(xx), "--", label="Floater-Hormann") >>> ax.plot(xx, p(xx), "--", label="Polynomial") >>> ax.legend() >>> plt.show()