solve_bvp#
- scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0, bc_tol=None)[source]#
Solve a boundary value problem for a system of ODEs.
This function numerically solves a first order system of ODEs subject to two-point boundary conditions:
dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b bc(y(a), y(b), p) = 0
Here x is a 1-D independent variable, y(x) is an n-D vector-valued function and p is a k-D vector of unknown parameters which is to be found along with y(x). For the problem to be determined, there must be n + k boundary conditions, i.e., bc must be an (n + k)-D function.
The last singular term on the right-hand side of the system is optional. It is defined by an n-by-n matrix S, such that the solution must satisfy S y(a) = 0. This condition will be forced during iterations, so it must not contradict boundary conditions. See [2] for the explanation how this term is handled when solving BVPs numerically.
Problems in a complex domain can be solved as well. In this case, y and p are considered to be complex, and f and bc are assumed to be complex-valued functions, but x stays real. Note that f and bc must be complex differentiable (satisfy Cauchy-Riemann equations [4]), otherwise you should rewrite your problem for real and imaginary parts separately. To solve a problem in a complex domain, pass an initial guess for y with a complex data type (see below).
- Parameters:
- funcallable
Right-hand side of the system. The calling signature is
fun(x, y), orfun(x, y, p)if parameters are present. All arguments are ndarray:xwith shape (m,),ywith shape (n, m), meaning thaty[:, i]corresponds tox[i], andpwith shape (k,). The return value must be an array with shape (n, m) and with the same layout asy.- bccallable
Function evaluating residuals of the boundary conditions. The calling signature is
bc(ya, yb), orbc(ya, yb, p)if parameters are present. All arguments are ndarray:yaandybwith shape (n,), andpwith shape (k,). The return value must be an array with shape (n + k,).- xarray_like, shape (m,)
Initial mesh. Must be a strictly increasing sequence of real numbers with
x[0]=aandx[-1]=b.- yarray_like, shape (n, m)
Initial guess for the function values at the mesh nodes, ith column corresponds to
x[i]. For problems in a complex domain pass y with a complex data type (even if the initial guess is purely real).- parray_like with shape (k,) or None, optional
Initial guess for the unknown parameters. If None (default), it is assumed that the problem doesn’t depend on any parameters.
- Sarray_like with shape (n, n) or None
Matrix defining the singular term. If None (default), the problem is solved without the singular term.
- fun_jaccallable or None, optional
Function computing derivatives of f with respect to y and p. The calling signature is
fun_jac(x, y), orfun_jac(x, y, p)if parameters are present. The return must contain 1 or 2 elements in the following order:df_dy : array_like with shape (n, n, m), where an element (i, j, q) equals to d f_i(x_q, y_q, p) / d (y_q)_j.
df_dp : array_like with shape (n, k, m), where an element (i, j, q) equals to d f_i(x_q, y_q, p) / d p_j.
Here q numbers nodes at which x and y are defined, whereas i and j number vector components. If the problem is solved without unknown parameters, df_dp should not be returned.
If fun_jac is None (default), the derivatives will be estimated by the forward finite differences.
- bc_jaccallable or None, optional
Function computing derivatives of bc with respect to ya, yb, and p. The calling signature is
bc_jac(ya, yb), orbc_jac(ya, yb, p)if parameters are present. The return must contain 2 or 3 elements in the following order:dbc_dya : array_like with shape (n, n), where an element (i, j) equals to d bc_i(ya, yb, p) / d ya_j.
dbc_dyb : array_like with shape (n, n), where an element (i, j) equals to d bc_i(ya, yb, p) / d yb_j.
dbc_dp : array_like with shape (n, k), where an element (i, j) equals to d bc_i(ya, yb, p) / d p_j.
If the problem is solved without unknown parameters, dbc_dp should not be returned.
If bc_jac is None (default), the derivatives will be estimated by the forward finite differences.
- tolfloat, optional
Desired tolerance of the solution. If we define
r = y' - f(x, y), where y is the found solution, then the solver tries to achieve on each mesh intervalnorm(r / (1 + abs(f)) < tol, wherenormis estimated in a root mean squared sense (using a numerical quadrature formula). Default is 1e-3.- max_nodesint, optional
Maximum allowed number of the mesh nodes. If exceeded, the algorithm terminates. Default is 1000.
- verbose{0, 1, 2}, optional
Level of algorithm’s verbosity:
0 (default) : work silently.
1 : display a termination report.
2 : display progress during iterations.
- bc_tolfloat, optional
Desired absolute tolerance for the boundary condition residuals: bc value should satisfy
abs(bc) < bc_tolcomponent-wise. Equals to tol by default. Up to 10 iterations are allowed to achieve this tolerance.
- Returns:
- Bunch object with the following fields defined:
- solPPoly
Found solution for y as
scipy.interpolate.PPolyinstance, a C1 continuous cubic spline.- pndarray or None, shape (k,)
Found parameters. None, if the parameters were not present in the problem.
- xndarray, shape (m,)
Nodes of the final mesh.
- yndarray, shape (n, m)
Solution values at the mesh nodes.
- ypndarray, shape (n, m)
Solution derivatives at the mesh nodes.
- rms_residualsndarray, shape (m - 1,)
RMS values of the relative residuals over each mesh interval (see the description of tol parameter).
- niterint
Number of completed iterations.
- statusint
Reason for algorithm termination:
0: The algorithm converged to the desired accuracy.
1: The maximum number of mesh nodes is exceeded.
2: A singular Jacobian encountered when solving the collocation system.
- messagestring
Verbal description of the termination reason.
- successbool
True if the algorithm converged to the desired accuracy (
status=0).
Notes
This function implements a 4th order collocation algorithm with the control of residuals similar to [1]. A collocation system is solved by a damped Newton method with an affine-invariant criterion function as described in [3].
Note that in [1] integral residuals are defined without normalization by interval lengths. So, their definition is different by a multiplier of h**0.5 (h is an interval length) from the definition used here.
Added in version 0.18.0.
Array API Standard Support
solve_bvphas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
⛔
PyTorch
⛔
⛔
JAX
⛔
⛔
Dask
⛔
n/a
See Support for the array API standard for more information.
References
[1] (1,2)J. Kierzenka, L. F. Shampine, “A BVP Solver Based on Residual Control and the Maltab PSE”, ACM Trans. Math. Softw., Vol. 27, Number 3, pp. 299-316, 2001.
[2]L.F. Shampine, P. H. Muir and H. Xu, “A User-Friendly Fortran BVP Solver”, J. Numer. Anal., Ind. Appl. Math. (JNAIAM), Vol. 1, Number 2, pp. 201-217, 2006.
[3]U. Ascher, R. Mattheij and R. Russell “Numerical Solution of Boundary Value Problems for Ordinary Differential Equations”, Philidelphia, PA: Society for Industrial and Applied Mathematics, 1995. DOI:10.1137/1.9781611971231
[4]Cauchy-Riemann equations on Wikipedia.
Examples
In the first example, we solve Bratu’s problem:
y'' + k * exp(y) = 0 y(0) = y(1) = 0
for k = 1.
We rewrite the equation as a first-order system and implement its right-hand side evaluation:
y1' = y2 y2' = -exp(y1)
>>> import numpy as np >>> def fun(x, y): ... return np.vstack((y[1], -np.exp(y[0])))
Implement evaluation of the boundary condition residuals:
>>> def bc(ya, yb): ... return np.array([ya[0], yb[0]])
Define the initial mesh with 5 nodes:
>>> x = np.linspace(0, 1, 5)
This problem is known to have two solutions. To obtain both of them, we use two different initial guesses for y. We denote them by subscripts a and b.
>>> y_a = np.zeros((2, x.size)) >>> y_b = np.zeros((2, x.size)) >>> y_b[0] = 3
Now we are ready to run the solver.
>>> from scipy.integrate import solve_bvp >>> res_a = solve_bvp(fun, bc, x, y_a) >>> res_b = solve_bvp(fun, bc, x, y_b)
Let’s plot the two found solutions. We take an advantage of having the solution in a spline form to produce a smooth plot.
>>> x_plot = np.linspace(0, 1, 100) >>> y_plot_a = res_a.sol(x_plot)[0] >>> y_plot_b = res_b.sol(x_plot)[0] >>> import matplotlib.pyplot as plt >>> plt.plot(x_plot, y_plot_a, label='y_a') >>> plt.plot(x_plot, y_plot_b, label='y_b') >>> plt.legend() >>> plt.xlabel("x") >>> plt.ylabel("y") >>> plt.show()
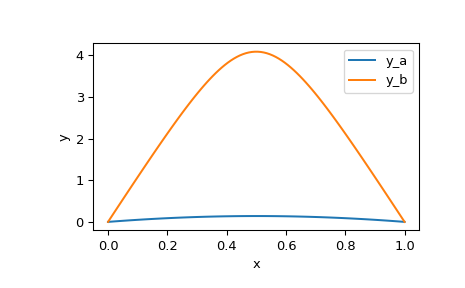
We see that the two solutions have similar shape, but differ in scale significantly.
In the second example, we solve a simple Sturm-Liouville problem:
y'' + k**2 * y = 0 y(0) = y(1) = 0
It is known that a non-trivial solution y = A * sin(k * x) is possible for k = pi * n, where n is an integer. To establish the normalization constant A = 1 we add a boundary condition:
y'(0) = k
Again, we rewrite our equation as a first-order system and implement its right-hand side evaluation:
y1' = y2 y2' = -k**2 * y1
>>> def fun(x, y, p): ... k = p[0] ... return np.vstack((y[1], -k**2 * y[0]))
Note that parameters p are passed as a vector (with one element in our case).
Implement the boundary conditions:
>>> def bc(ya, yb, p): ... k = p[0] ... return np.array([ya[0], yb[0], ya[1] - k])
Set up the initial mesh and guess for y. We aim to find the solution for k = 2 * pi, to achieve that we set values of y to approximately follow sin(2 * pi * x):
>>> x = np.linspace(0, 1, 5) >>> y = np.zeros((2, x.size)) >>> y[0, 1] = 1 >>> y[0, 3] = -1
Run the solver with 6 as an initial guess for k.
>>> sol = solve_bvp(fun, bc, x, y, p=[6])
We see that the found k is approximately correct:
>>> sol.p[0] 6.28329460046
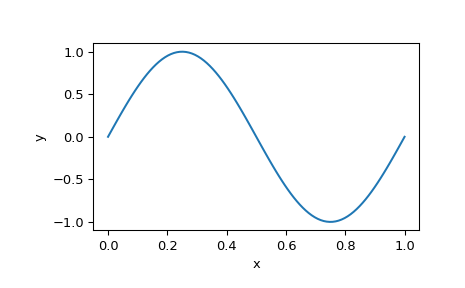
And, finally, plot the solution to see the anticipated sinusoid:
>>> x_plot = np.linspace(0, 1, 100) >>> y_plot = sol.sol(x_plot)[0] >>> plt.plot(x_plot, y_plot) >>> plt.xlabel("x") >>> plt.ylabel("y") >>> plt.show()