scipy.special.laguerre

scipy.special.laguerre(n, monic=False)

Laguerre polynomial.

Defined to be the solution of

\[x\frac{d^2}{dx^2}L_n + (1 - x)\frac{d}{dx}L_n + nL_n = 0;\]

\(L_n\) is a polynomial of degree \(n\).

Parameters

nint

Degree of the polynomial.

monicbool, optional

If True, scale the leading coefficient to be 1. Default is False.

Returns

Lorthopoly1d

Laguerre Polynomial.

See also

genlaguerre

Generalized (associated) Laguerre polynomial.

Notes

The polynomials \(L_n\) are orthogonal over \([0, \infty)\) with weight function \(e^{-x}\).

References

AS

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Examples

The Laguerre polynomials \(L_n\) are the special case \(\alpha = 0\) of the generalized Laguerre polynomials \(L_n^{(\alpha)}\). Let’s verify it on the interval \([-1, 1]\):

>>> from scipy.special import genlaguerre
>>> from scipy.special import laguerre
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> np.allclose(genlaguerre(3, 0)(x), laguerre(3)(x))
True

The polynomials \(L_n\) also satisfy the recurrence relation:

\[(n + 1)L_{n+1}(x) = (2n +1 -x)L_n(x) - nL_{n-1}(x)\]

This can be easily checked on \([0, 1]\) for \(n = 3\):

>>> from scipy.special import laguerre
>>> x = np.arange(0.0, 1.0, 0.01)
>>> np.allclose(4 * laguerre(4)(x),
...             (7 - x) * laguerre(3)(x) - 3 * laguerre(2)(x))
True

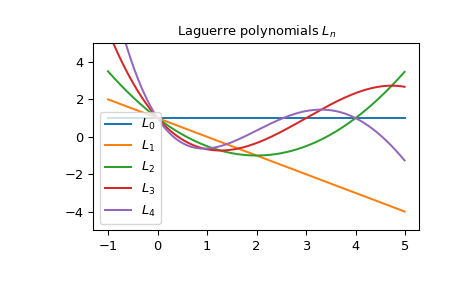
This is the plot of the first few Laguerre polynomials \(L_n\):

>>> import matplotlib.pyplot as plt
>>> from scipy.special import laguerre
>>> x = np.arange(-1.0, 5.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-5.0, 5.0)
>>> ax.set_title(r'Laguerre polynomials $L_n$')
>>> for n in np.arange(0, 5):
...     ax.plot(x, laguerre(n)(x), label=rf'$L_{n}$')
>>> plt.legend(loc='best')
>>> plt.show()

previous

scipy.special.jacobi

next

scipy.special.genlaguerre