numpy.linalg.qr

numpy.linalg.qr(a, mode='full')

Compute the qr factorization of a matrix.

Factor the matrix a as qr, where q is orthonormal (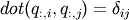, the Kronecker delta) and r is upper-triangular.

Parameters:

a : array_like, shape (M, N)

Matrix to be factored.

mode : {‘full’, ‘r’, ‘economic’}

Specifies the information to be returned. ‘full’ is the default. mode=’r’ returns a “true” r, while ‘economic’ returns a “polluted” r (albeit slightly faster; see Returns below).

Returns:

* If mode = ‘full’: :

• q : ndarray of float or complex, shape (M, K)
• r : ndarray of float or complex, shape (K, N)

Size K = min(M, N)

* If mode = ‘r’: :

• r : ndarray of float or complex, shape (K, N)

* If mode = ‘economic’: :

• a2 : ndarray of float or complex, shape (M, N)

The diagonal and the upper triangle of a2 contains r, while the rest of the matrix is undefined.

Raises:

LinAlgError :

If factoring fails.

Notes

This is an interface to the LAPACK routines dgeqrf, zgeqrf, dorgqr, and zungqr.

For more information on the qr factorization, see for example: http://en.wikipedia.org/wiki/QR_factorization

Subclasses of ndarray are preserved, so if a is of type matrix, all the return values will be matrices too.

Examples

>>> a = np.random.randn(9, 6)
>>> q, r = np.linalg.qr(a)
>>> np.allclose(a, np.dot(q, r))  # a does equal qr
True
>>> r2 = np.linalg.qr(a, mode='r')
>>> r3 = np.linalg.qr(a, mode='economic')
>>> np.allclose(r, r2)  # mode='r' returns the same r as mode='full'
True
>>> # But only triu parts are guaranteed equal when mode='economic'
>>> np.allclose(r, np.triu(r3[:6,:6], k=0))
True

Example illustrating a common use of qr: solving of least squares problems

What are the least-squares-best m and y0 in y = y0 + mx for the following data: {(0,1), (1,0), (1,2), (2,1)}. (Graph the points and you’ll see that it should be y0 = 0, m = 1.) The answer is provided by solving the over-determined matrix equation Ax = b, where:

A = array([[0, 1], [1, 1], [1, 1], [2, 1]])
x = array([[y0], [m]])
b = array([[1], [0], [2], [1]])

If A = qr such that q is orthonormal (which is always possible via Gram-Schmidt), then x = inv(r) * (q.T) * b. (In numpy practice, however, we simply use lstsq.)

>>> A = np.array([[0, 1], [1, 1], [1, 1], [2, 1]])
>>> A
array([[0, 1],
       [1, 1],
       [1, 1],
       [2, 1]])
>>> b = np.array([1, 0, 2, 1])
>>> q, r = LA.qr(A)
>>> p = np.dot(q.T, b)
>>> np.dot(LA.inv(r), p)
array([  1.1e-16,   1.0e+00])