numpy.linalg.cholesky

numpy.linalg.cholesky(a)

Cholesky decomposition.

Return the Cholesky decomposition, L * L.H, of the square matrix a, where L is lower-triangular and .H is the conjugate transpose operator (which is the ordinary transpose if a is real-valued). a must be Hermitian (symmetric if real-valued) and positive-definite. Only L is actually returned.

Parameters:

a : array_like, shape (M, M)

Hermitian (symmetric if all elements are real), positive-definite input matrix.

Returns:

L : ndarray, or matrix object if a is, shape (M, M)

Lower-triangular Cholesky factor of a.

Raises:

LinAlgError :

If the decomposition fails, for example, if a is not positive-definite.

Notes

The Cholesky decomposition is often used as a fast way of solving

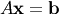
(when A is both Hermitian/symmetric and positive-definite).

First, we solve for 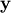in

and then for 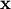in

Examples

>>> A = np.array([[1,-2j],[2j,5]])
>>> A
array([[ 1.+0.j,  0.-2.j],
       [ 0.+2.j,  5.+0.j]])
>>> L = np.linalg.cholesky(A)
>>> L
array([[ 1.+0.j,  0.+0.j],
       [ 0.+2.j,  1.+0.j]])
>>> np.dot(L, L.T.conj()) # verify that L * L.H = A
array([[ 1.+0.j,  0.-2.j],
       [ 0.+2.j,  5.+0.j]])
>>> A = [[1,-2j],[2j,5]] # what happens if A is only array_like?
>>> np.linalg.cholesky(A) # an ndarray object is returned
array([[ 1.+0.j,  0.+0.j],
       [ 0.+2.j,  1.+0.j]])
>>> # But a matrix object is returned if A is a matrix object
>>> LA.cholesky(np.matrix(A))
matrix([[ 1.+0.j,  0.+0.j],
        [ 0.+2.j,  1.+0.j]])