scipy.interpolate.approximate_taylor_polynomial

scipy.interpolate.approximate_taylor_polynomial(f, x, degree, scale, order=None)

Estimate the Taylor polynomial of f at x by polynomial fitting.

Parameters

fcallable

The function whose Taylor polynomial is sought. Should accept a vector of x values.

xscalar

The point at which the polynomial is to be evaluated.

degreeint

The degree of the Taylor polynomial

scalescalar

The width of the interval to use to evaluate the Taylor polynomial. Function values spread over a range this wide are used to fit the polynomial. Must be chosen carefully.

orderint or None, optional

The order of the polynomial to be used in the fitting; f will be evaluated order+1 times. If None, use degree.

Returns

ppoly1d instance

The Taylor polynomial (translated to the origin, so that for example p(0)=f(x)).

Notes

The appropriate choice of “scale” is a trade-off; too large and the function differs from its Taylor polynomial too much to get a good answer, too small and round-off errors overwhelm the higher-order terms. The algorithm used becomes numerically unstable around order 30 even under ideal circumstances.

Choosing order somewhat larger than degree may improve the higher-order terms.

Examples

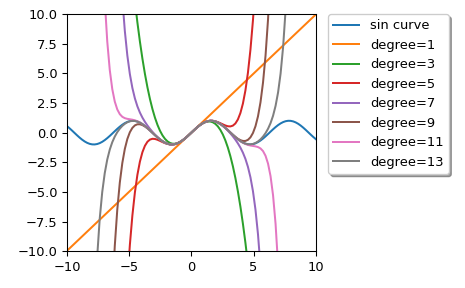
We can calculate Taylor approximation polynomials of sin function with various degrees:

>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import approximate_taylor_polynomial
>>> x = np.linspace(-10.0, 10.0, num=100)
>>> plt.plot(x, np.sin(x), label="sin curve")
>>> for degree in np.arange(1, 15, step=2):
...     sin_taylor = approximate_taylor_polynomial(np.sin, 0, degree, 1,
...                                                order=degree + 2)
...     plt.plot(x, sin_taylor(x), label=f"degree={degree}")
>>> plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left',
...            borderaxespad=0.0, shadow=True)
>>> plt.tight_layout()
>>> plt.axis([-10, 10, -10, 10])
>>> plt.show()