scipy.stats.boxcox#

scipy.stats.boxcox(x, lmbda=None, alpha=None, optimizer=None)[source]#

Return a dataset transformed by a Box-Cox power transformation.

Parameters

xndarray

Input array. Must be positive 1-dimensional. Must not be constant.

lmbda{None, scalar}, optional

If lmbda is not None, do the transformation for that value. If lmbda is None, find the lambda that maximizes the log-likelihood function and return it as the second output argument.

alpha{None, float}, optional

If alpha is not None, return the 100 * (1-alpha)% confidence interval for lmbda as the third output argument. Must be between 0.0 and 1.0.

optimizercallable, optional

If lmbda is None, optimizer is the scalar optimizer used to find the value of lmbda that minimizes the negative log-likelihood function. optimizer is a callable that accepts one argument:

funcallable: The objective function, which evaluates the negative log-likelihood function at a provided value of lmbda

and returns an object, such as an instance of scipy.optimize.OptimizeResult, which holds the optimal value of lmbda in an attribute x.

See the example in boxcox_normmax or the documentation of scipy.optimize.minimize_scalar for more information.

If lmbda is not None, optimizer is ignored.

Returns

boxcoxndarray: Box-Cox power transformed array.
maxlogfloat, optional: If the lmbda parameter is None, the second returned argument is the lambda that maximizes the log-likelihood function.
(min_ci, max_ci)tuple of float, optional: If lmbda parameter is None and alpha is not None, this returned tuple of floats represents the minimum and maximum confidence limits given alpha.

See also

probplot, boxcox_normplot, boxcox_normmax, boxcox_llf

Notes

The Box-Cox transform is given by:

y = (x**lmbda - 1) / lmbda,  for lmbda != 0
    log(x),                  for lmbda = 0

boxcox requires the input data to be positive. Sometimes a Box-Cox transformation provides a shift parameter to achieve this; boxcox does not. Such a shift parameter is equivalent to adding a positive constant to x before calling boxcox.

The confidence limits returned when alpha is provided give the interval where:

\[llf(\hat{\lambda}) - llf(\lambda) < \frac{1}{2}\chi^2(1 - \alpha, 1),\]

with llf the log-likelihood function and \(\chi^2\) the chi-squared function.

References

G.E.P. Box and D.R. Cox, “An Analysis of Transformations”, Journal of the Royal Statistical Society B, 26, 211-252 (1964).

Examples

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

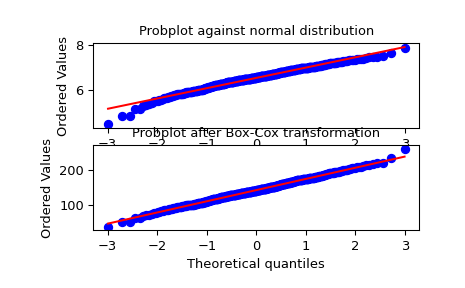
We generate some random variates from a non-normal distribution and make a probability plot for it, to show it is non-normal in the tails:

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

We now use boxcox to transform the data so it’s closest to normal:

>>> ax2 = fig.add_subplot(212)
>>> xt, _ = stats.boxcox(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Box-Cox transformation')

>>> plt.show()

scipy.stats.mstats.rsh

scipy.stats.boxcox_normmax