scipy.special.eval_legendre#

scipy.special.eval_legendre(n, x, out=None) = <ufunc 'eval_legendre'>#

Evaluate Legendre polynomial at a point.

The Legendre polynomials can be defined via the Gauss hypergeometric function \({}_2F_1\) as

\[P_n(x) = {}_2F_1(-n, n + 1; 1; (1 - x)/2).\]

When \(n\) is an integer the result is a polynomial of degree \(n\). See 22.5.49 in [AS] for details.

Parameters

narray_like: Degree of the polynomial. If not an integer, the result is determined via the relation to the Gauss hypergeometric function.
xarray_like: Points at which to evaluate the Legendre polynomial

Returns

See also

References

AS: Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Examples

>>> from scipy.special import eval_legendre

Evaluate the zero-order Legendre polynomial at x = 0

>>> eval_legendre(0, 0)
1.0

Evaluate the first-order Legendre polynomial between -1 and 1

>>> X = np.linspace(-1, 1, 5)  # Domain of Legendre polynomials
>>> eval_legendre(1, X)
array([-1. , -0.5,  0. ,  0.5,  1. ])

Evaluate Legendre polynomials of order 0 through 4 at x = 0

>>> N = range(0, 5)
>>> eval_legendre(N, 0)
array([ 1.   ,  0.   , -0.5  ,  0.   ,  0.375])

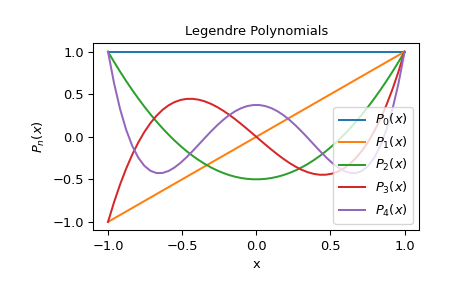
Plot Legendre polynomials of order 0 through 4

>>> X = np.linspace(-1, 1)

>>> import matplotlib.pyplot as plt
>>> for n in range(0, 5):
...     y = eval_legendre(n, X)
...     plt.plot(X, y, label=r'$P_{}(x)$'.format(n))

>>> plt.title("Legendre Polynomials")
>>> plt.xlabel("x")
>>> plt.ylabel(r'$P_n(x)$')
>>> plt.legend(loc='lower right')
>>> plt.show()

scipy.special.assoc_laguerre

scipy.special.eval_chebyt