Multivariate data interpolation on a regular grid (RegularGridInterpolator)#
Suppose you have N-dimensional data on a regular grid, and you
want to interpolate it. In such a case, RegularGridInterpolator can be
useful. Several interpolation strategies are supported: nearest-neighbor,
linear, and tensor product splines of odd degree.
Strictly speaking, this class efficiently handles data given on rectilinear grids: hypercubic lattices with possibly unequal spacing between points. The number of points per dimension can be different for different dimensions.
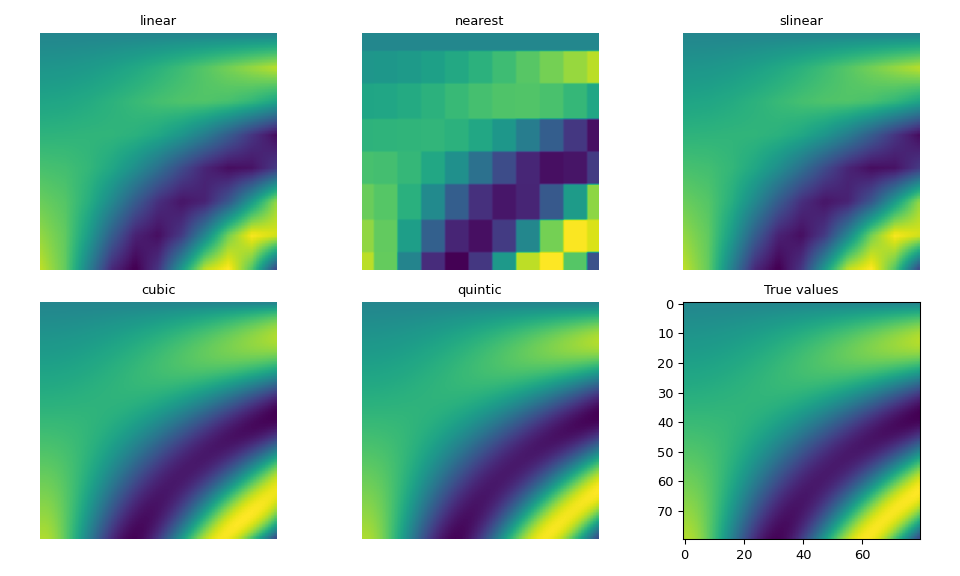
The following example demonstrates its use, and compares the interpolation results using each method.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import RegularGridInterpolator
Suppose we want to interpolate this 2-D function.
>>> def F(u, v):
... return u * np.cos(u * v) + v * np.sin(u * v)
Suppose we only know some data on a regular grid.
>>> fit_points = [np.linspace(0, 3, 8), np.linspace(0, 3, 11)]
>>> values = F(*np.meshgrid(*fit_points, indexing='ij'))
Creating test points and true values for evaluations.
>>> ut, vt = np.meshgrid(np.linspace(0, 3, 80), np.linspace(0, 3, 80), indexing='ij')
>>> true_values = F(ut, vt)
>>> test_points = np.array([ut.ravel(), vt.ravel()]).T
We can create the interpolator and interpolate test points using each method.
>>> interp = RegularGridInterpolator(fit_points, values)
>>> fig, axes = plt.subplots(2, 3, figsize=(10, 6))
>>> axes = axes.ravel()
>>> fig_index = 0
>>> for method in ['linear', 'nearest', 'slinear', 'cubic', 'quintic']:
... im = interp(test_points, method=method).reshape(80, 80)
... axes[fig_index].imshow(im)
... axes[fig_index].set_title(method)
... axes[fig_index].axis("off")
... fig_index += 1
>>> axes[fig_index].imshow(true_values)
>>> axes[fig_index].set_title("True values")
>>> fig.tight_layout()
>>> fig.show()
As expected, the higher degree spline interpolations are closest to the true values, though are more expensive to compute than with linear or nearest. The slinear interpolation also matches the linear interpolation.
If your data is such that spline methods produce ringing, you may consider
using method=”pchip”, which uses the tensor product of PCHIP interpolators,
a PchipInterpolator per dimension.
If you prefer a functional interface opposed to explicitly creating a class instance,
the interpn convenience function offers the equivalent functionality.
Specifically, these two forms give identical results:
>>> from scipy.interpolate import interpn
>>> rgi = RegularGridInterpolator(fit_points, values)
>>> result_rgi = rgi(test_points)
and
>>> result_interpn = interpn(fit_points, values, test_points)
>>> np.allclose(result_rgi, result_interpn, atol=1e-15)
True
For data confined to an (N-1)-dimensional subspace of N-dimensional space, i.e.
when one of the grid axes has length 1, the extrapolation along this axis is
controlled by the fill_value keyword parameter:
>>> x = np.array([0, 5, 10])
>>> y = np.array([0])
>>> data = np.array([[0], [5], [10]])
>>> rgi = RegularGridInterpolator((x, y), data,
... bounds_error=False, fill_value=None)
>>> rgi([(2, 0), (2, 1), (2, -1)]) # extrapolates the value on the axis
array([2., 2., 2.])
>>> rgi.fill_value = -101
>>> rgi([(2, 0), (2, 1), (2, -1)])
array([2., -101., -101.])
Note
If the input data is such that input dimensions have incommensurate units and differ by many orders of magnitude, the interpolant may have numerical artifacts. Consider rescaling the data before interpolating.
Uniformly spaced data#
If you are dealing with data on Cartesian grids with integer coordinates, e.g.
resampling image data, these routines may not be the optimal choice. Consider
using scipy.ndimage.map_coordinates instead.
For floating-point data on grids with equal spacing, map_coordinates can
be easily wrapped into a RegularGridInterpolator look-alike. The following is
a bare-bones example originating from the Johanness Buchner’s
‘regulargrid’ package:
class CartesianGridInterpolator:
def __init__(self, points, values, method='linear'):
self.limits = np.array([[min(x), max(x)] for x in points])
self.values = np.asarray(values, dtype=float)
self.order = {'linear': 1, 'cubic': 3, 'quintic': 5}[method]
def __call__(self, xi):
"""
`xi` here is an array-like (an array or a list) of points.
Each "point" is an ndim-dimensional array_like, representing
the coordinates of a point in ndim-dimensional space.
"""
# transpose the xi array into the ``map_coordinates`` convention
# which takes coordinates of a point along columns of a 2D array.
xi = np.asarray(xi).T
# convert from data coordinates to pixel coordinates
ns = self.values.shape
coords = [(n-1)*(val - lo) / (hi - lo)
for val, n, (lo, hi) in zip(xi, ns, self.limits)]
# interpolate
return map_coordinates(self.values, coords,
order=self.order,
cval=np.nan) # fill_value
This wrapper can be used as a(n almost) drop-in replacement for the
RegularGridInterpolator:
>>> x, y = np.arange(5), np.arange(6)
>>> xx, yy = np.meshgrid(x, y, indexing='ij')
>>> values = xx**3 + yy**3
>>> rgi = RegularGridInterpolator((x, y), values, method='linear')
>>> rgi([[1.5, 1.5], [3.5, 2.6]])
array([ 9. , 64.9])
>>> cgi = CartesianGridInterpolator((x, y), values, method='linear')
array([ 9. , 64.9])
Note that the example above uses the map_coordinates boundary conditions.
Thus, results of the cubic and quintic interpolations may differ from
those of the RegularGridInterpolator.
Refer to scipy.ndimage.map_coordinates documentation for more details on
boundary conditions and other additional arguments.
Finally, we note that this simplified example assumes that the input data is
given in the ascending order.