scipy.special.gdtrc

scipy.special.gdtrc(a, b, x, out=None) = <ufunc 'gdtrc'>

Gamma distribution survival function.

Integral from x to infinity of the gamma probability density function,

\[F = \int_x^\infty \frac{a^b}{\Gamma(b)} t^{b-1} e^{-at}\,dt,\]

where \(\Gamma\) is the gamma function.

Parameters:

aarray_like

The rate parameter of the gamma distribution, sometimes denoted \(\beta\) (float). It is also the reciprocal of the scale parameter \(\theta\).

barray_like

The shape parameter of the gamma distribution, sometimes denoted \(\alpha\) (float).

xarray_like

The quantile (lower limit of integration; float).

outndarray, optional

Optional output array for the function values

Returns:

Fscalar or ndarray

The survival function of the gamma distribution with parameters a and b evaluated at x.

See also

gdtr

Gamma distribution cumulative distribution function

scipy.stats.gamma

Gamma distribution

gdtrix

Notes

The evaluation is carried out using the relation to the incomplete gamma integral (regularized gamma function).

Wrapper for the Cephes [1] routine gdtrc. Calling gdtrc directly can improve performance compared to the sf method of scipy.stats.gamma (see last example below).

References

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Examples

Compute the function for a=1 and b=2 at x=5.

>>> import numpy as np
>>> from scipy.special import gdtrc
>>> import matplotlib.pyplot as plt
>>> gdtrc(1., 2., 5.)
0.04042768199451279

Compute the function for a=1, b=2 at several points by providing a NumPy array for x.

>>> xvalues = np.array([1., 2., 3., 4])
>>> gdtrc(1., 1., xvalues)
array([0.36787944, 0.13533528, 0.04978707, 0.01831564])

gdtrc can evaluate different parameter sets by providing arrays with broadcasting compatible shapes for a, b and x. Here we compute the function for three different a at four positions x and b=3, resulting in a 3x4 array.

>>> a = np.array([[0.5], [1.5], [2.5]])
>>> x = np.array([1., 2., 3., 4])
>>> a.shape, x.shape
((3, 1), (4,))

>>> gdtrc(a, 3., x)
array([[0.98561232, 0.9196986 , 0.80884683, 0.67667642],
       [0.80884683, 0.42319008, 0.17357807, 0.0619688 ],
       [0.54381312, 0.12465202, 0.02025672, 0.0027694 ]])

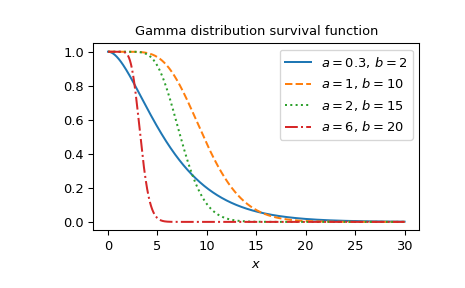
Plot the function for four different parameter sets.

>>> a_parameters = [0.3, 1, 2, 6]
>>> b_parameters = [2, 10, 15, 20]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(a_parameters, b_parameters, linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     a, b, style = parameter_set
...     gdtrc_vals = gdtrc(a, b, x)
...     ax.plot(x, gdtrc_vals, label=f"$a= {a},\, b={b}$", ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("Gamma distribution survival function")
>>> plt.show()

The gamma distribution is also available as scipy.stats.gamma. Using gdtrc directly can be much faster than calling the sf method of scipy.stats.gamma, especially for small arrays or individual values. To get the same results one must use the following parametrization: stats.gamma(b, scale=1/a).sf(x)=gdtrc(a, b, x).

>>> from scipy.stats import gamma
>>> a = 2
>>> b = 3
>>> x = 1.
>>> gdtrc_result = gdtrc(a, b, x)  # this will often be faster than below
>>> gamma_dist_result = gamma(b, scale=1/a).sf(x)
>>> gdtrc_result == gamma_dist_result  # test that results are equal
True