scipy.signal.welch

scipy.signal.welch(x, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, average='mean')

Estimate power spectral density using Welch’s method.

Welch’s method [1] computes an estimate of the power spectral density by dividing the data into overlapping segments, computing a modified periodogram for each segment and averaging the periodograms.

Parameters:

xarray_like

Time series of measurement values

fsfloat, optional

Sampling frequency of the x time series. Defaults to 1.0.

windowstr or tuple or array_like, optional

Desired window to use. If window is a string or tuple, it is passed to get_window to generate the window values, which are DFT-even by default. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a Hann window.

npersegint, optional

Length of each segment. Defaults to None, but if window is str or tuple, is set to 256, and if window is array_like, is set to the length of the window.

noverlapint, optional

Number of points to overlap between segments. If None, noverlap = nperseg // 2. Defaults to None.

nfftint, optional

Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.

detrendstr or function or False, optional

Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to the detrend function. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to ‘constant’.

return_onesidedbool, optional

If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Defaults to True, but for complex data, a two-sided spectrum is always returned.

scaling{ ‘density’, ‘spectrum’ }, optional

Selects between computing the power spectral density (‘density’) where Pxx has units of V**2/Hz and computing the power spectrum (‘spectrum’) where Pxx has units of V**2, if x is measured in V and fs is measured in Hz. Defaults to ‘density’

axisint, optional

Axis along which the periodogram is computed; the default is over the last axis (i.e. axis=-1).

average{ ‘mean’, ‘median’ }, optional

Method to use when averaging periodograms. Defaults to ‘mean’.

New in version 1.2.0.

Returns:

fndarray

Array of sample frequencies.

Pxxndarray

Power spectral density or power spectrum of x.

See also

periodogram

Simple, optionally modified periodogram

lombscargle

Lomb-Scargle periodogram for unevenly sampled data

Notes

An appropriate amount of overlap will depend on the choice of window and on your requirements. For the default Hann window an overlap of 50% is a reasonable trade off between accurately estimating the signal power, while not over counting any of the data. Narrower windows may require a larger overlap.

If noverlap is 0, this method is equivalent to Bartlett’s method [2].

New in version 0.12.0.

References

[1]

P. Welch, “The use of the fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms”, IEEE Trans. Audio Electroacoust. vol. 15, pp. 70-73, 1967.

[2]

M.S. Bartlett, “Periodogram Analysis and Continuous Spectra”, Biometrika, vol. 37, pp. 1-16, 1950.

Examples

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Generate a test signal, a 2 Vrms sine wave at 1234 Hz, corrupted by 0.001 V**2/Hz of white noise sampled at 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2*np.sqrt(2)
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> x = amp*np.sin(2*np.pi*freq*time)
>>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)

Compute and plot the power spectral density.

>>> f, Pxx_den = signal.welch(x, fs, nperseg=1024)
>>> plt.semilogy(f, Pxx_den)
>>> plt.ylim([0.5e-3, 1])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('PSD [V**2/Hz]')
>>> plt.show()

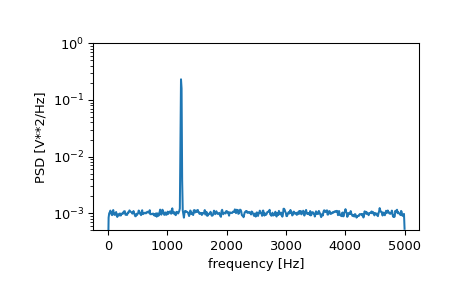
If we average the last half of the spectral density, to exclude the peak, we can recover the noise power on the signal.

>>> np.mean(Pxx_den[256:])
0.0009924865443739191

Now compute and plot the power spectrum.

>>> f, Pxx_spec = signal.welch(x, fs, 'flattop', 1024, scaling='spectrum')
>>> plt.figure()
>>> plt.semilogy(f, np.sqrt(Pxx_spec))
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Linear spectrum [V RMS]')
>>> plt.show()

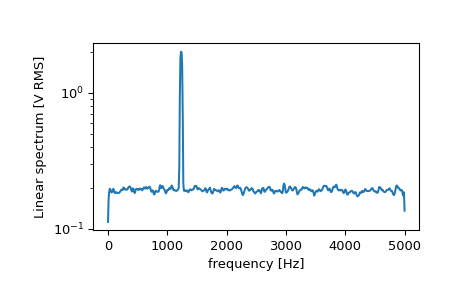
The peak height in the power spectrum is an estimate of the RMS amplitude.

>>> np.sqrt(Pxx_spec.max())
2.0077340678640727

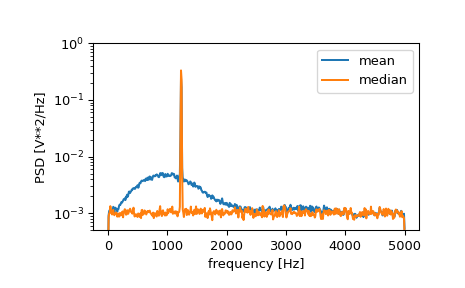
If we now introduce a discontinuity in the signal, by increasing the amplitude of a small portion of the signal by 50, we can see the corruption of the mean average power spectral density, but using a median average better estimates the normal behaviour.

>>> x[int(N//2):int(N//2)+10] *= 50.
>>> f, Pxx_den = signal.welch(x, fs, nperseg=1024)
>>> f_med, Pxx_den_med = signal.welch(x, fs, nperseg=1024, average='median')
>>> plt.semilogy(f, Pxx_den, label='mean')
>>> plt.semilogy(f_med, Pxx_den_med, label='median')
>>> plt.ylim([0.5e-3, 1])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('PSD [V**2/Hz]')
>>> plt.legend()
>>> plt.show()