scipy.optimize.bracket

scipy.optimize.bracket(func, xa=0.0, xb=1.0, args=(), grow_limit=110.0, maxiter=1000)

Bracket the minimum of the function.

Given a function and distinct initial points, search in the downhill direction (as defined by the initial points) and return new points xa, xb, xc that bracket the minimum of the function f(xa) > f(xb) < f(xc). It doesn’t always mean that obtained solution will satisfy xa<=x<=xb.

Parameters:

funccallable f(x,*args)

Objective function to minimize.

xa, xbfloat, optional

Bracketing interval. Defaults xa to 0.0, and xb to 1.0.

argstuple, optional

Additional arguments (if present), passed to func.

grow_limitfloat, optional

Maximum grow limit. Defaults to 110.0

maxiterint, optional

Maximum number of iterations to perform. Defaults to 1000.

Returns:

xa, xb, xcfloat

Bracket.

fa, fb, fcfloat

Objective function values in bracket.

funcallsint

Number of function evaluations made.

Examples

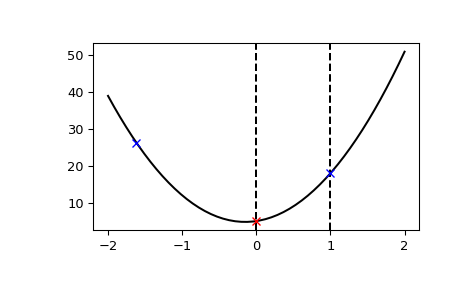
This function can find a downward convex region of a function:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import bracket
>>> def f(x):
...     return 10*x**2 + 3*x + 5
>>> x = np.linspace(-2, 2)
>>> y = f(x)
>>> init_xa, init_xb = 0, 1
>>> xa, xb, xc, fa, fb, fc, funcalls = bracket(f, xa=init_xa, xb=init_xb)
>>> plt.axvline(x=init_xa, color="k", linestyle="--")
>>> plt.axvline(x=init_xb, color="k", linestyle="--")
>>> plt.plot(x, y, "-k")
>>> plt.plot(xa, fa, "bx")
>>> plt.plot(xb, fb, "rx")
>>> plt.plot(xc, fc, "bx")
>>> plt.show()