numpy.random.mtrand.RandomState.multivariate_normal¶
- RandomState.multivariate_normal(mean, cov[, size])¶
Draw random samples from a multivariate normal distribution.
The multivariate normal, multinormal or Gaussian distribution is a generalisation of the one-dimensional normal distribution to higher dimensions.
Such a distribution is specified by its mean and covariance matrix, which are analogous to the mean (average or “centre”) and variance (standard deviation squared or “width”) of the one-dimensional normal distribution.
Parameters: mean : (N,) ndarray
Mean of the N-dimensional distribution.
cov : (N,N) ndarray
Covariance matrix of the distribution.
size : tuple of ints, optional
Given a shape of, for example, (m,n,k), m*n*k samples are generated, and packed in an m-by-n-by-k arrangement. Because each sample is N-dimensional, the output shape is (m,n,k,N). If no shape is specified, a single sample is returned.
Returns: out : ndarray
The drawn samples, arranged according to size. If the shape given is (m,n,...), then the shape of out is is (m,n,...,N).
In other words, each entry out[i,j,...,:] is an N-dimensional value drawn from the distribution.
Notes
The mean is a coordinate in N-dimensional space, which represents the location where samples are most likely to be generated. This is analogous to the peak of the bell curve for the one-dimensional or univariate normal distribution.
Covariance indicates the level to which two variables vary together. From the multivariate normal distribution, we draw N-dimensional samples,
![X = [x_1, x_2, ... x_N]](../../_images/math/8000a340636a80e715766ba653718435e467e3bb.png) . The covariance matrix
element
. The covariance matrix
element 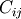 is the covariance of
is the covariance of 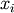 and
and 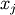 .
The element
.
The element 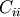 is the variance of
is the variance of 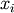 (i.e. its
“spread”).
(i.e. its
“spread”).Instead of specifying the full covariance matrix, popular approximations include:
- Spherical covariance (cov is a multiple of the identity matrix)
- Diagonal covariance (cov has non-negative elements, and only on the diagonal)
This geometrical property can be seen in two dimensions by plotting generated data-points:
>>> mean = [0,0] >>> cov = [[1,0],[0,100]] # diagonal covariance, points lie on x or y-axis
>>> import matplotlib.pyplot as plt >>> x,y = np.random.multivariate_normal(mean,cov,5000).T >>> plt.plot(x,y,'x'); plt.axis('equal'); plt.show()
Note that the covariance matrix must be non-negative definite.
References
[R204] A. Papoulis, “Probability, Random Variables, and Stochastic Processes,” 3rd ed., McGraw-Hill Companies, 1991 [R205] R.O. Duda, P.E. Hart, and D.G. Stork, “Pattern Classification,” 2nd ed., Wiley, 2001. Examples
>>> mean = (1,2) >>> cov = [[1,0],[1,0]] >>> x = np.random.multivariate_normal(mean,cov,(3,3)) >>> x.shape (3, 3, 2)
The following is probably true, given that 0.6 is roughly twice the standard deviation:
>>> print list( (x[0,0,:] - mean) < 0.6 ) [True, True]
