numpy.random.chisquare

numpy.random.chisquare(df, size=None)

Draw samples from a chi-square distribution.

When df independent random variables, each with standard normal distributions (mean 0, variance 1), are squared and summed, the resulting distribution is chi-square (see Notes). This distribution is often used in hypothesis testing.

Parameters:

df : int

Number of degrees of freedom.

size : tuple of ints, int, optional

Size of the returned array. By default, a scalar is returned.

Returns:

output : ndarray

Samples drawn from the distribution, packed in a size-shaped array.

Raises:

ValueError :

When df <= 0 or when an inappropriate size (e.g. size=-1) is given.

Notes

The variable obtained by summing the squares of df independent, standard normally distributed random variables:

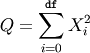
is chi-square distributed, denoted

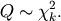
The probability density function of the chi-squared distribution is

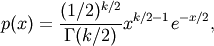
where 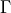is the gamma function,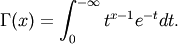

References

[R74]

NIST/SEMATECH e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/eda/section3/eda3666.htm

[R75]

Wikipedia, “Chi-square distribution”, http://en.wikipedia.org/wiki/Chi-square_distribution

Examples

>>> np.random.chisquare(2,4)
array([ 1.89920014,  9.00867716,  3.13710533,  5.62318272])