numpy.bartlett

numpy.bartlett(M)

Return the Bartlett window.

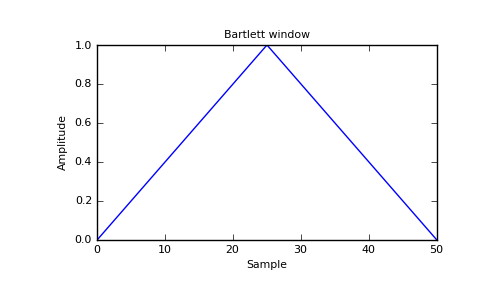
The Bartlett window is very similar to a triangular window, except that the end points are at zero. It is often used in signal processing for tapering a signal, without generating too much ripple in the frequency domain.

Parameters:

M : int

Number of points in the output window. If zero or less, an empty array is returned.

Returns:

out : array

The triangular window, normalized to one (the value one appears only if the number of samples is odd), with the first and last samples equal to zero.

See also

blackman, hamming, hanning, kaiser

Notes

The Bartlett window is defined as

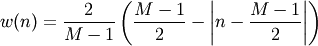
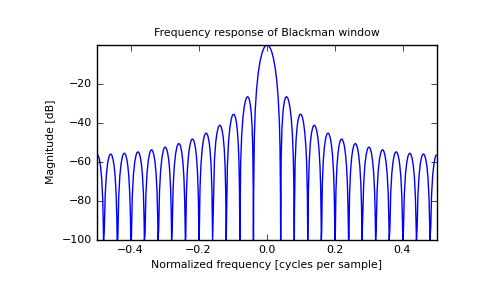
Most references to the Bartlett window come from the signal processing literature, where it is used as one of many windowing functions for smoothing values. Note that convolution with this window produces linear interpolation. It is also known as an apodization (which means”removing the foot”, i.e. smoothing discontinuities at the beginning and end of the sampled signal) or tapering function. The fourier transform of the Bartlett is the product of two sinc functions. Note the excellent discussion in Kanasewich.

References

[R18]

M.S. Bartlett, “Periodogram Analysis and Continuous Spectra”, Biometrika 37, 1-16, 1950.

[R19]

E.R. Kanasewich, “Time Sequence Analysis in Geophysics”, The University of Alberta Press, 1975, pp. 109-110.

[R20]

A.V. Oppenheim and R.W. Schafer, “Discrete-Time Signal Processing”, Prentice-Hall, 1999, pp. 468-471.

[R21]

Wikipedia, “Window function”, http://en.wikipedia.org/wiki/Window_function

[R22]

W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling, “Numerical Recipes”, Cambridge University Press, 1986, page 429.

Examples

>>> np.bartlett(12)
array([ 0.        ,  0.18181818,  0.36363636,  0.54545455,  0.72727273,
        0.90909091,  0.90909091,  0.72727273,  0.54545455,  0.36363636,
        0.18181818,  0.        ])

Plot the window and its frequency response (requires SciPy and matplotlib):

>>> from numpy import clip, log10, array, bartlett, linspace
>>> from numpy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = bartlett(51)
>>> plt.plot(window)
>>> plt.title("Bartlett window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")
>>> plt.show()

>>> plt.figure()
>>> A = fft(window, 2048) / 25.5
>>> mag = abs(fftshift(A))
>>> freq = linspace(-0.5,0.5,len(A))
>>> response = 20*log10(mag)
>>> response = clip(response,-100,100)
>>> plt.plot(freq, response)
>>> plt.title("Frequency response of Blackman window")
>>> plt.ylabel("Magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")
>>> plt.axis('tight')
>>> plt.show()

(Source code)

Output

(png, pdf)

(png, pdf)