scipy.stats.differential_entropy#

scipy.stats.differential_entropy(values, *, window_length=None, base=None, axis=0, method='auto')[source]#

Given a sample of a distribution, estimate the differential entropy.

Several estimation methods are available using the method parameter. By default, a method is selected based the size of the sample.

Parameters

valuessequence

Sample from a continuous distribution.

window_lengthint, optional

Window length for computing Vasicek estimate. Must be an integer between 1 and half of the sample size. If None (the default), it uses the heuristic value

\[\left \lfloor \sqrt{n} + 0.5 \right \rfloor\]

where \(n\) is the sample size. This heuristic was originally proposed in [2] and has become common in the literature.

basefloat, optional

The logarithmic base to use, defaults to e (natural logarithm).

axisint, optional

The axis along which the differential entropy is calculated. Default is 0.

method{‘vasicek’, ‘van es’, ‘ebrahimi’, ‘correa’, ‘auto’}, optional

The method used to estimate the differential entropy from the sample. Default is 'auto'. See Notes for more information.

Returns

entropyfloat: The calculated differential entropy.

Notes

This function will converge to the true differential entropy in the limit

\[n \to \infty, \quad m \to \infty, \quad \frac{m}{n} \to 0\]

The optimal choice of window_length for a given sample size depends on the (unknown) distribution. Typically, the smoother the density of the distribution, the larger the optimal value of window_length [1].

The following options are available for the method parameter.

'vasicek' uses the estimator presented in [1]. This is one of the first and most influential estimators of differential entropy.
'van es' uses the bias-corrected estimator presented in [3], which is not only consistent but, under some conditions, asymptotically normal.
'ebrahimi' uses an estimator presented in [4], which was shown in simulation to have smaller bias and mean squared error than the Vasicek estimator.
'correa' uses the estimator presented in [5] based on local linear regression. In a simulation study, it had consistently smaller mean square error than the Vasiceck estimator, but it is more expensive to compute.
'auto' selects the method automatically (default). Currently, this selects 'van es' for very small samples (<10), 'ebrahimi' for moderate sample sizes (11-1000), and 'vasicek' for larger samples, but this behavior is subject to change in future versions.

All estimators are implemented as described in [6].

References

1(1,2): Vasicek, O. (1976). A test for normality based on sample entropy. Journal of the Royal Statistical Society: Series B (Methodological), 38(1), 54-59.
2: Crzcgorzewski, P., & Wirczorkowski, R. (1999). Entropy-based goodness-of-fit test for exponentiality. Communications in Statistics-Theory and Methods, 28(5), 1183-1202.
3: Van Es, B. (1992). Estimating functionals related to a density by a class of statistics based on spacings. Scandinavian Journal of Statistics, 61-72.
4: Ebrahimi, N., Pflughoeft, K., & Soofi, E. S. (1994). Two measures of sample entropy. Statistics & Probability Letters, 20(3), 225-234.
5: Correa, J. C. (1995). A new estimator of entropy. Communications in Statistics-Theory and Methods, 24(10), 2439-2449.
6: Noughabi, H. A. (2015). Entropy Estimation Using Numerical Methods. Annals of Data Science, 2(2), 231-241. https://link.springer.com/article/10.1007/s40745-015-0045-9

Examples

>>> from scipy.stats import differential_entropy, norm

Entropy of a standard normal distribution:

>>> rng = np.random.default_rng()
>>> values = rng.standard_normal(100)
>>> differential_entropy(values)
1.3407817436640392

Compare with the true entropy:

>>> float(norm.entropy())
1.4189385332046727

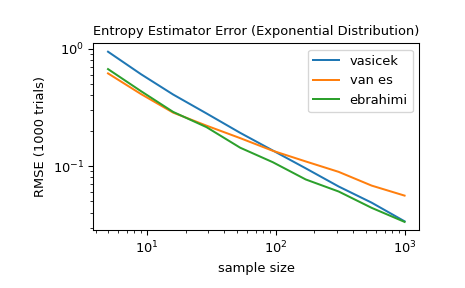
For several sample sizes between 5 and 1000, compare the accuracy of the 'vasicek', 'van es', and 'ebrahimi' methods. Specifically, compare the root mean squared error (over 1000 trials) between the estimate and the true differential entropy of the distribution.

>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>>
>>>
>>> def rmse(res, expected):
...     '''Root mean squared error'''
...     return np.sqrt(np.mean((res - expected)**2))
>>>
>>>
>>> a, b = np.log10(5), np.log10(1000)
>>> ns = np.round(np.logspace(a, b, 10)).astype(int)
>>> reps = 1000  # number of repetitions for each sample size
>>> expected = stats.expon.entropy()
>>>
>>> method_errors = {'vasicek': [], 'van es': [], 'ebrahimi': []}
>>> for method in method_errors:
...     for n in ns:
...        rvs = stats.expon.rvs(size=(reps, n), random_state=rng)
...        res = stats.differential_entropy(rvs, method=method, axis=-1)
...        error = rmse(res, expected)
...        method_errors[method].append(error)
>>>
>>> for method, errors in method_errors.items():
...     plt.loglog(ns, errors, label=method)
>>>
>>> plt.legend()
>>> plt.xlabel('sample size')
>>> plt.ylabel('RMSE (1000 trials)')
>>> plt.title('Entropy Estimator Error (Exponential Distribution)')

../../_images/scipy-stats-differential_entropy-1.png