scipy.interpolate.InterpolatedUnivariateSpline

class scipy.interpolate.InterpolatedUnivariateSpline(x, y, w=None, bbox=[None, None], k=3, ext=0, check_finite=False)

1-D interpolating spline for a given set of data points.

Fits a spline y = spl(x) of degree k to the provided x, y data. Spline function passes through all provided points. Equivalent to UnivariateSpline with s=0.

Parameters

x(N,) array_like

Input dimension of data points – must be strictly increasing

y(N,) array_like

input dimension of data points

w(N,) array_like, optional

Weights for spline fitting. Must be positive. If None (default), weights are all equal.

bbox(2,) array_like, optional

2-sequence specifying the boundary of the approximation interval. If None (default), bbox=[x[0], x[-1]].

kint, optional

Degree of the smoothing spline. Must be 1 <= k <= 5.

extint or str, optional

Controls the extrapolation mode for elements not in the interval defined by the knot sequence.

• if ext=0 or ‘extrapolate’, return the extrapolated value.

• if ext=1 or ‘zeros’, return 0

• if ext=2 or ‘raise’, raise a ValueError

• if ext=3 of ‘const’, return the boundary value.

The default value is 0.

check_finitebool, optional

Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination or non-sensical results) if the inputs do contain infinities or NaNs. Default is False.

See also

UnivariateSpline

a smooth univariate spline to fit a given set of data points.

LSQUnivariateSpline

a spline for which knots are user-selected

SmoothBivariateSpline

a smoothing bivariate spline through the given points

LSQBivariateSpline

a bivariate spline using weighted least-squares fitting

splrep

a function to find the B-spline representation of a 1-D curve

splev

a function to evaluate a B-spline or its derivatives

sproot

a function to find the roots of a cubic B-spline

splint

a function to evaluate the definite integral of a B-spline between two given points

spalde

a function to evaluate all derivatives of a B-spline

Notes

The number of data points must be larger than the spline degree k.

Examples

>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import InterpolatedUnivariateSpline
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
>>> spl = InterpolatedUnivariateSpline(x, y)
>>> plt.plot(x, y, 'ro', ms=5)
>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(xs, spl(xs), 'g', lw=3, alpha=0.7)
>>> plt.show()

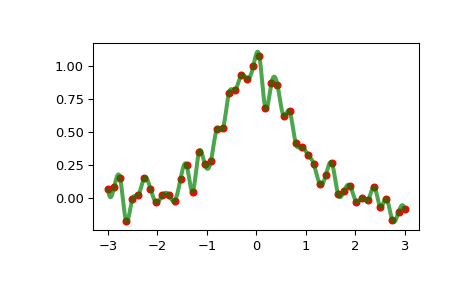
Notice that the spl(x) interpolates y:

>>> spl.get_residual()
0.0

Methods

__call__(x[, nu, ext])	Evaluate spline (or its nu-th derivative) at positions x.
antiderivative([n])	Construct a new spline representing the antiderivative of this spline.
derivative([n])	Construct a new spline representing the derivative of this spline.
derivatives(x)	Return all derivatives of the spline at the point x.
get_coeffs()	Return spline coefficients.
get_knots()	Return positions of interior knots of the spline.
get_residual()	Return weighted sum of squared residuals of the spline approximation.
integral(a, b)	Return definite integral of the spline between two given points.
roots()	Return the zeros of the spline.
set_smoothing_factor(s)	Continue spline computation with the given smoothing factor s and with the knots found at the last call.

validate_input