scipy.signal.iircomb

scipy.signal.iircomb(w0, Q, ftype='notch', fs=2.0)

Design IIR notching or peaking digital comb filter.

A notching comb filter is a band-stop filter with a narrow bandwidth (high quality factor). It rejects a narrow frequency band and leaves the rest of the spectrum little changed.

A peaking comb filter is a band-pass filter with a narrow bandwidth (high quality factor). It rejects components outside a narrow frequency band.

Parameters

w0float

Frequency to attenuate (notching) or boost (peaking). If fs is specified, this is in the same units as fs. By default, it is a normalized scalar that must satisfy 0 < w0 < 1, with w0 = 1 corresponding to half of the sampling frequency.

Qfloat

Quality factor. Dimensionless parameter that characterizes notch filter -3 dB bandwidth bw relative to its center frequency, Q = w0/bw.

ftype{‘notch’, ‘peak’}

The type of comb filter generated by the function. If ‘notch’, then it returns a filter with notches at frequencies 0, w0, 2 * w0, etc. If ‘peak’, then it returns a filter with peaks at frequencies 0.5 * w0, 1.5 * w0, 2.5 * w0`, etc. Default is ‘notch’.

fsfloat, optional

The sampling frequency of the signal. Default is 2.0.

Returns

b, andarray, ndarray

Numerator (b) and denominator (a) polynomials of the IIR filter.

Raises

ValueError

If w0 is less than or equal to 0 or greater than or equal to fs/2, if fs is not divisible by w0, if ftype is not ‘notch’ or ‘peak’

See also

iirnotch

iirpeak

Notes

For implementation details, see [1]. The TF implementation of the comb filter is numerically stable even at higher orders due to the use of a single repeated pole, which won’t suffer from precision loss.

References

1

Sophocles J. Orfanidis, “Introduction To Signal Processing”, Prentice-Hall, 1996

Examples

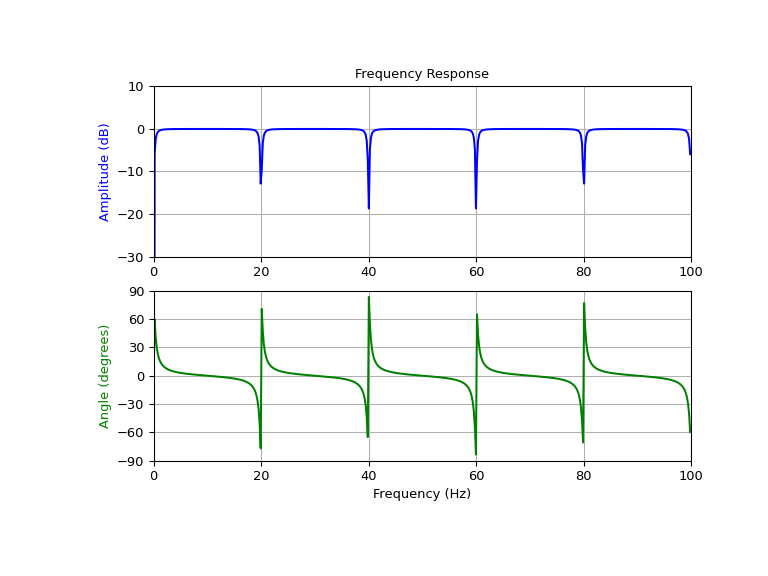
Design and plot notching comb filter at 20 Hz for a signal sampled at 200 Hz, using quality factor Q = 30

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> fs = 200.0  # Sample frequency (Hz)
>>> f0 = 20.0  # Frequency to be removed from signal (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design notching comb filter
>>> b, a = signal.iircomb(f0, Q, ftype='notch', fs=fs)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6))
>>> ax[0].plot(freq, 20*np.log10(abs(response)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude (dB)", color='blue')
>>> ax[0].set_xlim([0, 100])
>>> ax[0].set_ylim([-30, 10])
>>> ax[0].grid()
>>> ax[1].plot(freq, np.unwrap(np.angle(h))*180/np.pi, color='green')
>>> ax[1].set_ylabel("Angle (degrees)", color='green')
>>> ax[1].set_xlabel("Frequency (Hz)")
>>> ax[1].set_xlim([0, 100])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid()
>>> plt.show()

Design and plot peaking comb filter at 250 Hz for a signal sampled at 1000 Hz, using quality factor Q = 30

>>> fs = 1000.0  # Sample frequency (Hz)
>>> f0 = 250.0  # Frequency to be retained (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design peaking filter
>>> b, a = signal.iircomb(f0, Q, ftype='peak', fs=fs)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6))
>>> ax[0].plot(freq, 20*np.log10(np.maximum(abs(h), 1e-5)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude (dB)", color='blue')
>>> ax[0].set_xlim([0, 500])
>>> ax[0].set_ylim([-80, 10])
>>> ax[0].grid()
>>> ax[1].plot(freq, np.unwrap(np.angle(h))*180/np.pi, color='green')
>>> ax[1].set_ylabel("Angle (degrees)", color='green')
>>> ax[1].set_xlabel("Frequency (Hz)")
>>> ax[1].set_xlim([0, 500])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid()
>>> plt.show()

previous

scipy.signal.iirpeak

next

scipy.signal.lti