scipy.interpolate.UnivariateSpline¶
-
class
scipy.interpolate.UnivariateSpline(x, y, w=None, bbox=[None, None], k=3, s=None, ext=0, check_finite=False)[source]¶ 1-D smoothing spline fit to a given set of data points.
Fits a spline y = spl(x) of degree k to the provided x, y data. s specifies the number of knots by specifying a smoothing condition.
- Parameters
- x(N,) array_like
1-D array of independent input data. Must be increasing; must be strictly increasing if s is 0.
- y(N,) array_like
1-D array of dependent input data, of the same length as x.
- w(N,) array_like, optional
Weights for spline fitting. Must be positive. If None (default), weights are all equal.
- bbox(2,) array_like, optional
2-sequence specifying the boundary of the approximation interval. If None (default),
bbox=[x[0], x[-1]].- kint, optional
Degree of the smoothing spline. Must be 1 <= k <= 5. Default is k = 3, a cubic spline.
- sfloat or None, optional
Positive smoothing factor used to choose the number of knots. Number of knots will be increased until the smoothing condition is satisfied:
sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s
If None (default),
s = len(w)which should be a good value if1/w[i]is an estimate of the standard deviation ofy[i]. If 0, spline will interpolate through all data points.- extint or str, optional
Controls the extrapolation mode for elements not in the interval defined by the knot sequence.
if ext=0 or ‘extrapolate’, return the extrapolated value.
if ext=1 or ‘zeros’, return 0
if ext=2 or ‘raise’, raise a ValueError
if ext=3 of ‘const’, return the boundary value.
The default value is 0.
- check_finitebool, optional
Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination or non-sensical results) if the inputs do contain infinities or NaNs. Default is False.
See also
BivariateSplinea base class for bivariate splines.
SmoothBivariateSplinea smoothing bivariate spline through the given points
LSQBivariateSplinea bivariate spline using weighted least-squares fitting
RectSphereBivariateSplinea bivariate spline over a rectangular mesh on a sphere
SmoothSphereBivariateSplinea smoothing bivariate spline in spherical coordinates
LSQSphereBivariateSplinea bivariate spline in spherical coordinates using weighted least-squares fitting
RectBivariateSplinea bivariate spline over a rectangular mesh
InterpolatedUnivariateSplinea interpolating univariate spline for a given set of data points.
bisplrepa function to find a bivariate B-spline representation of a surface
bispleva function to evaluate a bivariate B-spline and its derivatives
splrepa function to find the B-spline representation of a 1-D curve
spleva function to evaluate a B-spline or its derivatives
sproota function to find the roots of a cubic B-spline
splinta function to evaluate the definite integral of a B-spline between two given points
spaldea function to evaluate all derivatives of a B-spline
Notes
The number of data points must be larger than the spline degree k.
NaN handling: If the input arrays contain
nanvalues, the result is not useful, since the underlying spline fitting routines cannot deal withnan. A workaround is to use zero weights for not-a-number data points:>>> from scipy.interpolate import UnivariateSpline >>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4]) >>> w = np.isnan(y) >>> y[w] = 0. >>> spl = UnivariateSpline(x, y, w=~w)
Notice the need to replace a
nanby a numerical value (precise value does not matter as long as the corresponding weight is zero.)Examples
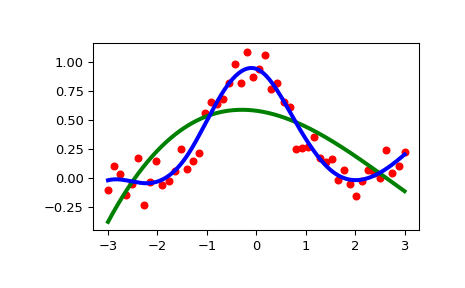
>>> import matplotlib.pyplot as plt >>> from scipy.interpolate import UnivariateSpline >>> x = np.linspace(-3, 3, 50) >>> y = np.exp(-x**2) + 0.1 * np.random.randn(50) >>> plt.plot(x, y, 'ro', ms=5)
Use the default value for the smoothing parameter:
>>> spl = UnivariateSpline(x, y) >>> xs = np.linspace(-3, 3, 1000) >>> plt.plot(xs, spl(xs), 'g', lw=3)
Manually change the amount of smoothing:
>>> spl.set_smoothing_factor(0.5) >>> plt.plot(xs, spl(xs), 'b', lw=3) >>> plt.show()
Methods
__call__(self, x[, nu, ext])Evaluate spline (or its nu-th derivative) at positions x.
antiderivative(self[, n])Construct a new spline representing the antiderivative of this spline.
derivative(self[, n])Construct a new spline representing the derivative of this spline.
derivatives(self, x)Return all derivatives of the spline at the point x.
get_coeffs(self)Return spline coefficients.
get_knots(self)Return positions of interior knots of the spline.
get_residual(self)Return weighted sum of squared residuals of the spline approximation.
integral(self, a, b)Return definite integral of the spline between two given points.
roots(self)Return the zeros of the spline.
set_smoothing_factor(self, s)Continue spline computation with the given smoothing factor s and with the knots found at the last call.
validate_input
